《两周自制脚本语言》笔记 3——LL(1) 语法分析及一个四则运算语言的实现

前面提到使用 BNF 来进行语法分析，实际上正则表达式也可用作语法表述，其能够表达部分 BNF 定义的语法（我们知道，正则表达式不能表达一些嵌套或递归的语法，比如括号匹配）。正则表达式表述的语法称为正则文法，BNF 表述的语法成为上下文无关文法。

正则用于字符串匹配，BNF 用于 Token 序列匹配，但若是将一个个字符作为 Token 看待，则 BNF 可以和正则本质相同——都是模式匹配。比如下面是一个例子。这里，number 可以是digit，可以是digit digit，可以是digit digit digit… 总之能够这样无限展开，无限递归下去。

1
2
3
[0-9]+ # 或 [0-9][0-9]*
digit: "0" | "1" | "2" | ... | "8" | "9"
number: digit | digit number # 使用 EBNF 的话就是 digit { digit } ……兄啊这不是数字啊

能够像 number 这样进行尾部递归，或者循环展开的定义都可以通过正则文法表示。但若是像expr : "(" expr ")" | ...这样的就无法通过正则表达了。

语法分析的算法

如果某种 BNF 定义的语法不是正则文法，则必须使用特定算法进行语法分析。

常见的语法分析算法可以分为向上分析算法和向下分析算法，其分别称为自底向上语法分析和自顶向下语法分析。

向上分析算法首先组合相邻单词，创建子表达式，并逐步组合，构造出整体结构，LR（Left-to-right，Rightmost derivation）算法是一个著名的自底向上分析算法，但其实现比较复杂。著名的 yacc 使用 LALR 语法分析。（gcc，JavaCC 使用什么算法？）

向下分析算法则是从整体结构开始向下分析。LL 语法分析（Left-to-right，Leftmost derivation）是其代表。LL 语法分析实现简单，是利用递归调用实现的递归下降语法分析器。

在学习编译原理时（我们好像只学了递归下降语法分析？），曾看到过 LL(1) 这样的术语，其意义为使用向下分析算法，但仅允许预读一次。LL(k) 似乎能满足大部分需要。关于预读的意义，这里先不阐述。

四则运算的 LL(1) 语法

下面对四则运算的 LL(1) 递归下降分析进行实现。

1
2
3
factor		:	NUMBER | "(" expr ")"
term		:	factor { ("*" | "/") factor }
expr		:	term { ("+" | "-") term }

再次确认——语法分析的意义是什么？生成抽象语法树。四则运算的抽象语法树是容易理解的——每一个子树都以加减乘除为根结点，以值为子树（或者只有一个值），其结果为一个值。

自底向下分析的大体流程是什么？前面说到，是“从整体结构向下分析”。也就是说，首先将源代码（Token 序列）看作一个整体——在这里当然是 expr 了，然后通过这个整体不断细分，尝试划分出更细的“单元”，这个过程同时也是不断构造 AST 的过程，直到完全由终结符组成。

一个栗子

其的代码实现也是容易的——每个非终结符都对应一个函数/方法，其将试图获取 Token，查看其是否匹配其对应的模式。其中，{}和|元符号也是能够转换成相应的代码模式的。比如，下面展示了 term 方法。

1
2
3
4
5
6
7
8
9
public ASTree term() {
    ASTree leftOrRootTree = factor(); // 根据 BNF 来的。这里故意使用了长命名，因为 term 可能有两种情况——如果后面接了操作符，则这个变量将为生成的 AST 的左结点（为什么？因为四则运算符的语法树就是这样！），如果后面没接操作符，那么这个变量的值就为生成 AST 的根结点
    while (isToken("*") || isToken("/")) {
        ASTree op = new ASTree(readAToken());
        ASTree right = factor();
        leftOrRootTree = new BinaryExpr(leftOrRootTree, op, right); // 递归定义，无论哪次迭代，leftOrRootTree 总为根结点，而前次的 leftOrRootTree 则为本次的左子树。
    }
    return leftOrRootTree;
}

该方法首先调用 factor 方法——对 factor 非终结符进行识别的方法。这方法将会通过词法分析器读取一个或多个 Token 并试图获取一个 factor。获取后返回结果——也就是说，它是有副作用的（！）。

需要注意的是，读取 Token 后，词法分析器的“指针”将会移动。isToken 方法除外——它只负责“瞧”一下指针当前所处位置的 Token。

获取一个 factor 后，其有两种可能——这个 term 已经结束了，可直接返回；这 term 还有内容，需要进一步操作。究竟是哪种可能，看一眼其后的 token 便可——如果它是乘号或除号，则必定仍旧有内容，需要继续操作。

看来，在编写语法分析树的时候，需要考虑最后拿到的 Token 要生成怎样的 AST。就比如这里操作符是放在中间的，如果是 lisp 那样的前缀表达式，运算符就放到第一个了（但生成的 AST 还是一样的）

具体实现

下面是四则运算的语法分析器的全部代码。在这里，所谓的预读指的就是 peek 方法。为了能够进行分支，语法分析必须进行预读。这里只调用了 peek(0)——其的意义是获取下一个会获取到的 Token，**因此该实现为 LL(1)**。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
// 负责四则运算的语法分析器——实际工作中不应当使用这种方式，而是通过工具生成
// 这里不为 Token 进行更复杂抽象——书中抽象出了双目运算符进行使用，仅通过原始 ASTree 对象进行使用。
// 这里的 AST 是一个典型的二叉树，节点的值为 Token
public class ExprParser {
    private Lexer lexer;
    public ExprParser(Lexer lexer) {
        this.lexer = lexer;
    }
    public ASTree parse() {
        return expr();
    }

	// expr		:	term { ("+" | "-") term }
    public ASTree expr() {
        ASTree leftOrRootTree = term();
        while (isIdentifierNamed("+") || isIdentifierNamed("-")) {
            Token op = lexer.read();
            ASTree right = term();
            leftOrRootTree = new ASTree(op, leftOrRootTree, right);
        }
        return leftOrRootTree;
    }
        
	// term		:	factor { ("*" | "/") factor }
    public ASTree term() {
        ASTree leftOrRootTree = factor();
        while (isIdentifierNamed("*") || isIdentifierNamed("/")) {
            Token op = lexer.read();
            ASTree right = factor();
            leftOrRootTree = new ASTree(op, leftOrRootTree, right);
        }
        return leftOrRootTree;
    }
    // factor		:	NUMBER | "(" expr ")"
    public ASTree factor() {
        Token nextToken = lexer.peek(0);
        if (nextToken.isNumber()) return new ASTree(lexer.read());
        ignoreToken("(");
        ASTree tree = expr();
        ignoreToken(")");
        return tree;
    }
    private void ignoreToken(String tokenName) {
        if (isIdentifierNamed(tokenName))
            lexer.read();
        else throw new LSException("ignored Token have false Name " + tokenName);
    }
    private boolean isIdentifierNamed(String name) {
        Token currentToken = lexer.peek(0);
        return currentToken.isIdentifier() && currentToken.getText().equals(name);
    }

    public static void main(String[] args) {
        ASTree tree = new ExprParser(Lexer.fromLines(new String[]{"(1+2)*3+4"})).parse();
        System.out.println(ExprEvaluator.eval(tree));
    }
}

下面是对 AST 进行解释的代码，其实现是非常容易的——对二叉树后序遍历并运算。这过程实际上是进行语义分析并执行的过程。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
public class ExprEvaluator {
    public static int eval(ASTree tree) {
        if (tree.isLeaf()) return tree.getValue().getNumber();
        int leftValue = eval(tree.getLeft());
        int rightValue = eval(tree.getRight());
        String op = tree.getValue().getText();
        switch (op) {
            case "+":
                return leftValue + rightValue;
            case "-":
                return leftValue - rightValue;
            case "*":
                return leftValue * rightValue;
            case "/":
                return leftValue / rightValue;
            default:
                throw new RuntimeException("这不可能！");
        }
    }
}

关于数学运算和表达式运算，还存在一种名为算符优先分析法（operator precedence parsing），其是一个弱化的 LR(1)，非常适合用来对表达式进行语法分析，实际上其也在很多情况下嵌入到自底向下语法分析器中。但是这里先不赘述了。

关于实现中的问题

一个需要注意的地方是，这里生成的 AST 的结构是固定的二叉树——根结点为操作符，左右两个子树为值，这样的结构是和四则运算的规律紧紧耦合的。复杂语言的 AST 是不能这样的——它一般来说不是二叉树，且计算所需信息一般都存储在子节点中。这时，根结点就负责表示 AST 节点的类型（这也意味着其的处理方法被规定了）。

AST 树中每个节点都有其类型，有其计算法。比如，一个 if 语句块的 AST 可能这样表示——

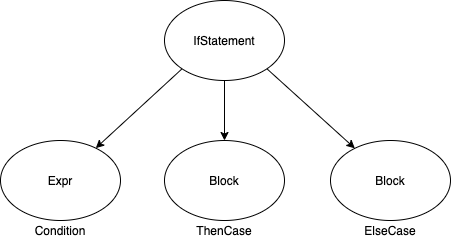
标识双目运算的 AST 可能这样表示——

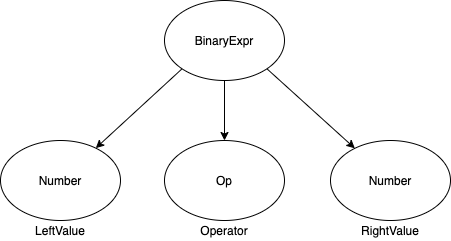
面对这样的树，它的计算方法是容易编写的，下面试图编写 IfStatement 的 eval 方法，其中 children 为子树的 List。

1
2
3
4
5
6
7
8
9
10
Result eval(ASTree ifStatement) {
    if (ifStatement.children.get(0).eval()) { // Condition 的值
        eval(ifStatement.children.get(1));
    } else {
        if (Statement.children.length == 3) { // 如果有 elseCase
            eval(ifStatement.children.get(2));
        }
    }
    return UnitResult; // If 对 Java 来说没有返回值
}

关于下一步的目标，我打算学习 stone 中的语法分析器（的生成器）的实现，编写一个内部 DSL 用以生成语法分析器代码。这流程是复杂的，可能是难以实现，需要借助外力（指书上的实现）的，但是学习它是有趣的 w。

本想先继续跟着它的进度来，然后发现了一个麻烦的问题——我用的抽象结构和它的不一样，导致不能直接使用它提供的 Parser，这搞得有点尴尬。现在考虑跟着另一本书《自制编译器》进行学习，在完成后回过头来，从头再来，带着自己更为深刻的理解重新学习。

还是继续吧，从它的代码继续——我可不想再次重蹈当初学习并发编程的覆辙了。