
为啥学这玩意?
翻伊月クロ老师的本子时,发现他上调子完全只使用墨汁(纯黑)和网点,没有任何灰度,发现这种方式能很快出效果且很有味道,又意识到网点对打印机友好,将来要是打印自己的作品的话会很方便,不需要很好的打印机。
然后找到一个网点的笔刷,绘制时发现难以保证纯黑白的基础上做渐变(就像刮刀),下面是最终得到的效果和实现方式的说明,基本原理是对网点的滤镜应用一个有明显渐变的纯黑白的不透明度蒙版(在 ps 里是剪切蒙版?),即做一个减法。


- 绘制网点
- 在网点下方建立一个图层,填充一个颜色
- 应用噪声滤镜,级别调到最高,生成就像电视没台时的噪声图
- 在噪声图层上创建一个图层,混合模式调整为线性光 Linear Light,它是线性减淡(相加)和线性加深(相乘、正片叠底)的混合,在亮度大于 0.5 时使用相加,小于 0.5 时使用线性加深
- 修改前景色为纯黑,背景色为纯白,在该图层拉一个前景色到背景色的渐变
- 合并这两个图层,做一个阈值滤镜,调整至边缘位置合适;渐变的拉的方式和阈值的设置会影响边缘的位置和柔软程度
- 将该图层转换为不透明度蒙版,置于网点图层下,bingo
将图层中的每一个像素看作一个 0-1 之间的数字,将阈值看作布尔化(变为 0,1),将相加和相乘模式看作数字的相加相减,上述的过程是非常容易理解的。
现在还是放弃了研究网点的想法了,原因是这玩意更适用于打印,在屏幕上缩放级别的不同会影响灰度,而显然后者现在是更主要的受众。但不能说白费功夫了,研究实现该效果的过程中熟悉了图层,蒙版,混合模式等概念并建立了相应心智模型,同时意识到我以前光把着画笔工具不放的想法和行为是多么睿智。
然后发现 krita 允许通过 SeExpr 这门脚本语言进行绘图,其中有两个效果超级炫酷的示例(第一张简直壮观),引起了我很强烈的兴趣:


要是能在背景,材质等地方使用这样酷炫的材质岂不美哉?于是就来到这里了。然而 SeExpr 的学习材料实在太少(全互联网有 10 篇吗?),这里只得去拿和它思想一致的 glsl 来动手动脚。这里跟随 https://thebookofshaders.com/?lan=ch 进行学习。SeExpr 的用法应当参考 https://docs.krita.org/zh_CN/reference_manual/seexpr.html(Krita 的官方文档是好东西,值得反反复复看 10 遍)。本打算每个例子都用 SeExpr 实现一下,但是懒了。先把画画画好再说!
glsl 是什么
glsl 与其说是编程语言,不如说是 DSL;glsl 语法和数据类型类似 C,glsl 脚本被交付给 GPU,在每一个像素上执行,用于修改该像素的颜色。可以认为 glsl 是一个接受像素坐标(和一些其他参数,称为 uniform;根据 GPU 的架构的性质,对每一个像素,uniform 的值均一致且不可变)的函数,返回像素颜色的函数,在这里,像素坐标是二元组,分别为 x,y 轴坐标(其实是四元组,但我们只看二维),其中原点在左下角;像素颜色为四元组,分别为 rgba 通道上的值。在 glsl 中,rgba 均使用 0-1 的浮点数表示,这种表示似乎称为 normalize 表示,它们乘以 255 会得到我们熟知的表示法。
下面是一个最简单的 glsl 脚本,它给整个画面从左到右做了一个黑白渐变:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
|
#ifdef GL_ES
precision mediump float;
#endif
uniform vec2 u_resolution;
void main() {
vec2 st = gl_FragCoord.xy / u_resolution;
gl_FragColor = vec4(vec3(st.x), 1.);
}
|

此外,glsl 支持 if-else,while,for(循环次数必须在“编译期”确定),三目表达式,但复杂语句可能会影响着色器性能,应尽量使用 glsl 提供的函数来完成功能,这些函数很多都是可以直接在硬件上执行的。
注意 glsl 很少会进行自动的类型转换,写浮点数时加上.是好习惯。
下面是另一个脚本,其使用了 distance 函数,绘制从中心开始的圆形渐变:
| #ifdef GL_ES
precision mediump float;
#endif
uniform vec2 u_resolution;
void main() {
vec2 coor = gl_FragCoord.xy/u_resolution;
float dist = distance(vec2(.5), coor) * 2.;
gl_FragColor = vec4(vec3(dist), 1);
}
|

教程关卡结束了!该来点烧脑子的东西了。下面的所有代码都有一个很大的问题——只考虑了画布为正方形的情况;但懒得研究了。
绘制函数汗背景
在 glsl 中,函数可视化有两种方式——使用灰度来表达 y 轴,或者使用 y 轴来表达 y 轴,前者就是绘制像上面第一个例子的黑白渐变,其就是通过灰度绘制了 y=x 的图像,后者就是在图像中实际绘制出函数曲线。
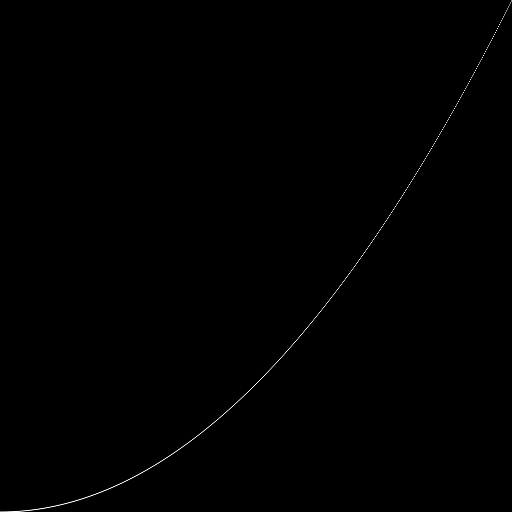
现在有个数学函数y=x^2,如何将它作为一条线绘制在画面上?具体来说就是,如何绘制这样的图像,它的大多数地方亮度为 0,该函数周围区域亮度为 1?
第一印象是,对每一个点,可以计算它到函数的距离,小于一定距离,则认为它在线上,绘制亮度为 1,否则绘制为 0,这里为了实现简单,只比较 y 轴方向的距离;代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| #ifdef GL_ES
precision mediump float;
#endif
uniform vec2 u_resolution;
bool isOnLine(vec2 st) {
float dist = distance(st, vec2(st.x, st.x * st.x));
return dist < 0.01;
}
void main() {
vec2 st = gl_FragCoord.xy/u_resolution;
gl_FragColor = vec4(vec3(isOnLine(st) ? 1. : 0.), 1.0);
}
|

这种方法有两个缺点,第一是函数导数大时函数会画得更细,反之会画得更粗;第二是绘制出来的线条的边缘会非常硬——从 1 直接跃迁到 0 了,中间没有任何渐变。
第一个问题先不考虑,看第二个问题,如何把它画的更平滑一些?我们需要一个类似阶梯函数但中间要有一个平滑但微小的过渡的东西,让它在距离大于特定值时返回 0,距离小于该特定值时返回 0-1 之间的数,更小时返回 1(处理这个“更小”和“特定值”就是处理函数边缘的硬度)。smoothstep 函数 满足我们的需求——它需要用户给定阶梯的开始和结束位置,通过某种插值法在中间生成平滑的过渡,下面是使用 smoothstep 函数来做的实现:
| #ifdef GL_ES
precision mediump float;
#endif
uniform vec2 u_resolution;
float plot(vec2 st) {
float dist = distance(st, vec2(st.x, st.x * st.x));
return smoothstep(0.002, 0., dist);
}
void main() {
vec2 st = gl_FragCoord.xy/u_resolution;
gl_FragColor = vec4(vec3(plot(st)), 1.0);
}
|
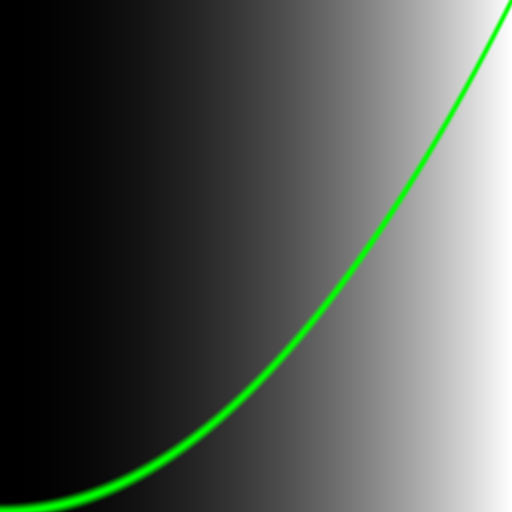
然后下一步,这函数的背景有点寡淡了,想给它加个背景,该怎么办?
考虑plot(st)的返回值,在大多数时候它返回 0,只有在函数附近时它才返回 1,我们的需求是,在 plot(st) 返回 0 的时候,显示背景色,在 plot(st) 返回 1 的时候显示前景色……在 plot(st) 在 0-1 之间的时候,返回前景色和背景色的混合……混合,混合……混合?
混合!答案实际上呼之欲出了——
| gl_FragColor = plot * lineColor + (1 - plot) * background;
|
背景色当然也可以是计算出来的,这里同时使用背景色和曲线来可视化y=x^2,下面使用功能相同的 mix 函数来进行混合:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| #ifdef GL_ES
precision mediump float;
#endif
uniform vec2 u_resolution;
float plot(vec2 st) {
float dist = distance(st, vec2(st.x, st.x * st.x));
return smoothstep(0.02, 0., dist);
}
void main() {
vec2 st = gl_FragCoord.xy/u_resolution;
vec3 background = vec3(st.x * st.x);
vec3 lineColor = vec3(0, 1, 0);
float plot = plot(st);
vec3 targetColor = vec3(mix(background, lineColor, plot));
gl_FragColor = vec4(targetColor, 1.);
}
|
组合图形
就像绘画时复杂的形体可以认为是简单的几何体的组合,使用 glsl 也可以组合不同的形状来绘制复杂图形;最简单的组合显然是加法(加法需要做一个clamp(0, 1)来保证最终的值仍然是归一化的)和乘法,分别对应求两个图形的并集和交集,比如下面就用四个图形的交集绘制一个矩形:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| #ifdef GL_ES
precision mediump float;
#endif
uniform vec2 u_resolution;
void main() {
vec2 st = gl_FragCoord.xy/u_resolution;
float color = 1.;
float left = step(.25, st.x);
float bottom = step(.25, st.y);
float right = step(st.x, .75);
float top = step(st.y, .75);
color *= left;
color *= bottom;
color *= right;
color *= top;
gl_FragColor = vec4(vec3(color),1.0);
}
|

该流程可以抽象成返回 float 的函数,返回 1 时表示需要绘制该图形,返回 0 时表示需要绘制背景,结合这样的函数和 mix 函数,就可以绘制多层的图像了,下面使用该方法临摹一幅抽象画:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
| #ifdef GL_ES
precision mediump float;
#endif
uniform vec2 u_resolution;
vec2 myStep(vec2 threshold, vec2 st) {
return floor(st - threshold) + 1.;
}
float rectangle(vec2 start, vec2 end, vec2 st) {
vec2 realStart = vec2(min(start.x, end.x), min(start.y, end.y));
vec2 realEnd = vec2(max(start.x, end.x), max(start.y, end.y));
vec2 bl = step(realStart, st);
vec2 tr = 1. - step(realEnd, st);
return bl.x * bl.y * tr.x * tr.y;
}
void main(){
vec2 st = gl_FragCoord.xy/u_resolution.xy;
vec3 background = vec3(247., 239., 220.) / 255.;
vec3 red = vec3(170., 40., 40.) / 255.;
vec3 orange = vec3(250., 195., 68.) / 255.;
vec3 skyBlue = vec3(17., 83., 140.) / 255.;
vec3 black = vec3(19., 19., 24.) / 255.;
vec3 color = background;
color = mix(color, red, rectangle(vec2(0.,1.), vec2(0.260,0.590), st));
color = mix(color, orange, rectangle(vec2(0.920,0.590), vec2(1.), st));
color = mix(color, skyBlue, rectangle(vec2(0.730,-1.000), vec2(1.000,0.120), st));
color = mix(color, black, rectangle(vec2(0.220,0.000), vec2(0.260,1.0), st));
color = mix(color, black, rectangle(vec2(0.730,-0.010), vec2(0.77,1.0), st));
color = mix(color, black, rectangle(vec2(0.910,-0.020), vec2(0.95,1.0), st));
color = mix(color, black, rectangle(vec2(0.,0.590), vec2(1.000,0.640), st));
color = mix(color, black, rectangle(vec2(0., 0.790), vec2(1.000,0.840), st));
color = mix(color, black, rectangle(vec2(0.220,0.090), vec2(1.000,0.140), st));
gl_FragColor = vec4(color,1.0);
}
|

二维变换
首先定义一个在原点处绘制坐标系和绘制一个描边矩形的函数,方便后面做示例:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
| #define PI 3.14159265359
uniform vec2 u_resolution;
float rectangle(vec2 start, vec2 end, vec2 st) {
vec2 realStart = vec2(min(start.x, end.x), min(start.y, end.y));
vec2 realEnd = vec2(max(start.x, end.x), max(start.y, end.y));
vec2 bl = step(realStart, st);
vec2 tr = 1. - step(realEnd, st);
return bl.x * bl.y * tr.x * tr.y;
}
vec2 rotate(float angle, vec2 st) {
return mat2(cos(angle),-sin(angle),
sin(angle),cos(angle)) * st;
}
float coorSys(vec2 st) {
float xAxis = rectangle(vec2(-1., -.01), vec2(1.25, .01), st) + rectangle(vec2(.49, -.05), vec2(.51, .05), st) + rectangle(vec2(.99, -.1), vec2(1.01, .1), st);
float yAxis = rectangle(vec2(-.01, -1.), vec2(.01, 1.25), st) + rectangle(vec2(-.05, .49), vec2(.05, .51), st) + rectangle(vec2(-.1, .99), vec2(.1, 1.01), st);
vec2 arrowX = rotate(PI / -4., st - vec2(1.2, 0.));
vec2 arrowY = rotate(PI / 4., st - vec2(0., 1.2));
return clamp(0., 1., xAxis + yAxis + rectangle(vec2(0.), vec2(0.1), arrowX)+ rectangle(vec2(0.), vec2(0.1), arrowY));
}
float box(vec2 st) {
return clamp(0., 1., rectangle(vec2(-.26), vec2(.26), st) - rectangle(vec2(-.24), vec2(.24), st));
}
|
每次对坐标进行修改时,我们就是在进行二维变换,最简单的二维变换包括平移,旋转,缩放,工业上这玩意应该是用齐次矩阵做的,但这里图简单。
如何理解二维变换?可以认为,每次对原坐标做映射,得到一个新坐标时,就是创建了一个对画布(后面把它称为世界坐标系)的新的视图坐标系(就像对数组或表的视图)。前面的学习中,其实也是在视图坐标系中绘制,只是它们正巧和世界坐标系一致罢了。当然,也可以以视图去建立视图,前者会成为后者的世界坐标系,相对和绝对嘛。
对每个像素,我们首先拿到的是它的世界坐标系的位置,我们需要找到这个像素在视图中的位置,并从视图的角度检查需要绘制何种内容。比如,将整个坐标系向右上角移动 (1, 1)。我们尝试在 (0, 0) 处绘制方块时,实际上就是在问,世界坐标系的哪里是我们的 (0, 0)?
为此,需要找到世界坐标系到视图的映射,下面的几种二维变换,实际上都是根据相应参数找到这样一个映射。
这个心智模型颇有些奇怪,第一印象是找到视图到世界坐标系的映射,但在这里似乎不适用,因为 glsl 做的是对世界坐标系的每一个坐标,检查它要画什么,而不是我要在(视图的)某个坐标画什么。前者的话,坐标的变换流程就会是 世界坐标系 -> 视图 1 -> 视图 2 -> 当前视图,后者的话就是当前视图 -> 视图 2 -> 视图 1 -> 世界坐标系。
实现了二维变换后,编写新的图形绘制函数的时候,只需要实现它在原点处的“单位”形状即可,后面的通过二维变换操作就行。
平移
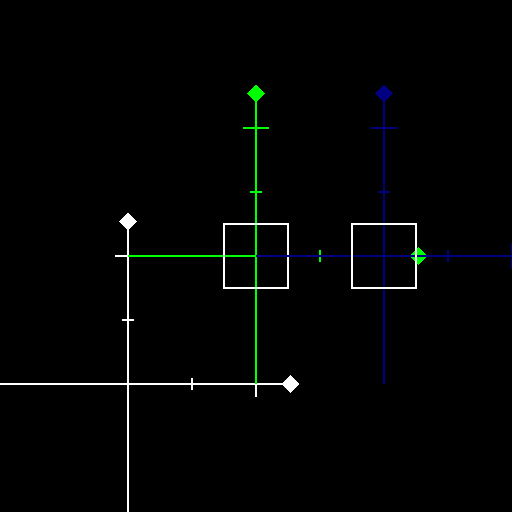
要将坐标系平移到 (1, 2),就需要以 (1, 2) 为原点建立一个坐标系,并始终在该坐标系下进行绘制,这样,代码在视图的 (0, 0) 处绘制时,实际上就是在世界坐标系的 (1, 2) 处绘制。
容易发现这样的对应关系:
| 世界坐标系 |
视图 |
| (0, 0) |
(-1, -2) |
| (1, 2) |
(0, 0) |
实现很显然了:
|
vec2 translate(vec2 dir, vec2 st) {
return st - dir;
}
|
下面的代码中利用平移在 (1, 1) 处绘制了一个矩形,并绘制了此时的视图坐标系。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
|
void draw(inout vec3 background, vec3 color, float pct) {
background = mix(background, color, pct);
}
void main() {
vec2 st = gl_FragCoord.xy/u_resolution;
st = st * 4. - 1.;
vec3 c = vec3(0.);
draw(c, vec3(1.), coorSys(st));
vec2 viewSt1 = translate(vec2(1.), st);
draw(c, vec3(0., 1., 0.), coorSys(viewSt1));
draw(c, vec3(1.), box(viewSt1));
vec2 viewSt2 = translate(vec2(1., 0.), viewSt1);
draw(c, vec3(0., 0., .5), coorSys(viewSt2));
draw(c, vec3(1.), box(viewSt2));
gl_FragColor = vec4(c,1.0);
}
|
旋转
旋转直接抄作业,总之是视图坐标系的旋转(恼),用初高中的知识应该就能推导出来,但我已经失掉这个能力了。实现和示例如下,移动到 (1, 1),然后再随时间旋转。
| vec2 rotate(float angle, vec2 st) {
return mat2(cos(angle),-sin(angle),
sin(angle),cos(angle)) * st;
}
void main() {
vec2 st = gl_FragCoord.xy/u_resolution;
st = st * 4. - 1.;
vec3 c = vec3(0.);
draw(c, vec3(1.), coorSys(st));
vec2 viewSt1 = translate(vec2(1.), st);
vec2 viewSt2 = rotate(u_time, viewSt1);
draw(c, vec3(.3, .3, .5), coorSys(viewSt2));
draw(c, vec3(1.), box(viewSt2));
gl_FragColor = vec4(c,1.0);
}
|

平移和旋转
同时使用平移和旋转时,平移和旋转的先后顺序会影响最终效果,但使用这套心智模型的话很容易理解它们的差异。
假设随时间旋转。先平移再旋转时,就是先向前走 10 步,然后原地转圈圈;先旋转再平移,就是在当前位置旋转,然后对每个角度,都向前走 10 步,它们的差别通过下面的例子可以看到;前者就是普通的原地转圈圈,后者类似月球围绕地球运动且潮汐锁定。
| void main() {
vec2 st = gl_FragCoord.xy/u_resolution;
st = st * 4. - 2.;
vec3 c = vec3(0.);
draw(c, vec3(1.), coorSys(st));
st = translate(vec2(0., 1.), st);
st = rotate(u_time, st);
draw(c, vec3(.3, .3, .5), coorSys(st));
draw(c, vec3(1.), box(st));
gl_FragColor = vec4(c,1.0);
}
|


缩放
缩放很好玩;如何把图形到原来的 2 倍呢?我们绘制图形还是同样的画,但需要这样一个效果,即我们在 (1, 0) 处绘制时,实际上要在 (2, 0) 处绘制,在 (2, 3) 处绘制时,实际上要在 (4, 6) 处绘制:
| 世界坐标系 |
视图 |
| (2, 0) |
(1, 0) |
| (4, 6) |
(2, 3) |
很显然了,实现和示例如下:
|
vec2 scale(float ratio, vec2 st) {
return st / ratio;
}
void main() {
vec2 st = gl_FragCoord.xy/u_resolution;
st = st * 4. - 2.;
vec3 c = vec3(0.);
draw(c, vec3(1.), coorSys(st));
st = translate(vec2(1.1), st);
st = scale(abs(sin(u_time)) * 2., st);
draw(c, vec3(.3, .3, .5), coorSys(st));
draw(c, vec3(1.), box(st));
gl_FragColor = vec4(c,1.0);
}
|

距离场
距离场是画面上任意一点同特定点的距离相关联的场,距离可以使用亮度来表示,距离越远,亮度越大。距离场并不是特定的几何图形,它是无穷大的,通过距离场来绘制各种东西是把它当作工具,而不是绘制它本身。利用距离场,能做出非常多有趣的效果,用途包括但不限于:
- 绘制硬边和软边圆形
- 绘制对称圆形,矩形,四角星
- 为上述的形状描边
注意下面的例子中使用 abs,max,min 等函数创建的视图。这个懒得截图了。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
| #ifdef GL_ES
precision mediump float;
#endif
uniform vec2 u_resolution;
float circle(vec2 c, float r, vec2 st) {
return 1. - step(r, distance(c, st));
}
void main(){
vec2 st = gl_FragCoord.xy/u_resolution.xy;
vec3 color = vec3(0.0);
float d = 0.0;
st = st *2.-1.;
d = length(st);
d = length(floor(st * 10.) / 10.);
gl_FragColor = vec4(vec3(d),1.0);
}
|

下面利用距离场和二维变换绘制了开头的 MyGo!!!!!! 的罗盘 logo,写得仓促,将就看。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
| #ifdef GL_ES
precision mediump float;
#endif
uniform vec2 u_resolution;
uniform float u_time;
#define PI 3.14159265359
vec2 translate(vec2 dir, vec2 st) {
return st - dir;
}
vec2 scale(vec2 ratio, vec2 st) {
return st / ratio;
}
vec2 rotate(float angle, vec2 st) {
return mat2(cos(angle),-sin(angle),
sin(angle),cos(angle)) * st;
}
void draw(inout vec3 background, vec3 color, float pct) {
background = mix(background, color, pct);
}
float shape0(vec2 st) {
if (st.x < 0. || st.y < 0.) return 0.;
float a = 2.414 * st.x - 0.589;
return clamp(0., 1., sign(st.y - a) - sign(st.y - st.x));
}
float dist2line(float k, float b, vec2 st) {
float x = st.x;
float y = st.y;
float A = k;
float B = -1.;
float C = b;
float dist = abs(A * x + B * y + C) / sqrt(A * A + B * B) ;
return dist;
}
float belowLine(float k, float b, vec2 st) {
return step(st.y - k * st.x - b, 0.);
}
float lb(vec2 x, vec2 st) {
vec2 r = step(st, vec2(x));
return r.x * r.y;
}
float drawPart(vec2 st) {
float test;
test += (step(0.691, length(st)) * step(length(st), 0.8333));
test = clamp(0., 1., test);
test += belowLine(-15. * PI / 180., 0.2557, st);
test = clamp(0., 1., test);
test = clamp(0., 1., clamp(0., 1., belowLine(-15. * PI / 180., 0.2557, vec2(st.y, st.x))) + test);
test = clamp(0., 1., test);
test += shape0(st) + shape0(vec2(st.y, st.x));
test = clamp(0., 1., test);
test -= clamp(0., 1., belowLine(-15. * PI / 180., 0.2083, vec2(st.x, st.y)));
test = clamp(0., 1., test);
test += belowLine(60. * PI / 180., 0., vec2(st.y, st.x)) * lb(vec2(.24), st);
test = clamp(0., 1., test);
return st.x < 0. || st.y < 0. ? 0. : test;
}
float myGo(vec2 st) {
float res;
res += drawPart(st);
st = rotate(90. * PI / 180., st);
res += drawPart(st);
st = rotate(90. * PI / 180., st);
res += drawPart(st);
st = rotate(90. * PI / 180., st);
res += drawPart(st);
st = rotate(90. * PI / 180., st);
return res;
}
void main() {
vec2 st = gl_FragCoord.xy/u_resolution;
vec3 blue = vec3(51., 124., 175.) / 255.;
st = st * 2. - 1.;
st = rotate(u_time, st);
vec3 c = blue;
draw(c, vec3(1.), myGo(st));
gl_FragColor = vec4(c,1.0);
}
|
模式
很多时候需要创建重复的图案,但是又不想挨个绘制,而是期待它们能自己就重复,使用 fract 函数创建的视图允许做到这一点。fract 函数获取浮点数的小数部分,只要将浮点数乘以 10,做个 fract,就能得到重复 10 次的图像:
| x(世界坐标系) |
x * 10 |
fract(x * 10)(视图) |
| 0.01 |
0.1 |
0.1 |
| 0.11 |
1.1 |
0.1 |
| 0.21 |
2.1 |
0.1 |
这样,只要我们在视图的 0.1 处绘图时,在 0.01,0.11,0.21 这三个坐标都能看到同样的结果,因为它们都对应着视图的 0.1。这样的每个重复的结果称为子空间。
一些例子如下。需要注意,在构造子空间前进行变换时,会对整个子空间进行变换,例子 2,3,4 都应用了这点;构造子空间后进行变换,则是分别对每个子空间进行变换。例子 4 结合了距离场做了一个渐变圆,这效果感觉画画时可以用到。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
| #ifdef GL_ES
precision mediump float;
#endif
uniform vec2 u_resolution;
uniform float u_time;
#define PI 3.14159265359
vec2 translate(vec2 dir, vec2 st) {
return st - dir;
}
vec2 scale(vec2 ratio, vec2 st) {
return st / ratio;
}
vec2 rotate(float angle, vec2 st) {
return mat2(cos(angle),-sin(angle),
sin(angle),cos(angle)) * st;
}
float box(vec2 st) {
vec2 bl = smoothstep(-0.5, -0.5+.01, st);
vec2 tr = smoothstep(0.5, 0.5-.01, st);
return bl.x * bl.y * tr.x * tr.y;
}
vec2 tile(float zoom, vec2 st) {
return fract(st * zoom);
}
void example0(out vec4 glFragColor, vec2 st) {
st = tile(10., st);
glFragColor = vec4(vec3(box(st)), 1.);
}
void example1(out vec4 glFragColor, float time, vec2 st) {
st = tile(10., st);
st = translate(vec2(.5), st);
st = scale(vec2(sqrt(2.) / 2.), st);
st = rotate(time, st);
glFragColor = vec4(vec3(box(st)), 1.);
}
void example2(out vec4 glFragColor, float time, vec2 st) {
st /= vec2(2.15,0.65)/1.5;
float TILE_NUM = 5.;
float isOdd = step(mod(st.y * TILE_NUM, 2.0), 1.);
st = translate(vec2(isOdd * .5 / TILE_NUM, .0), st);
st = tile(TILE_NUM, st);
st = translate(vec2(.5), st);
st = scale(vec2(.9), st);
glFragColor = vec4(vec3(box(st)), 1.);
}
void example3(out vec4 glFragColor, float time, vec2 st) {
float TILE_NUM = 10.;
float mode = step(1., mod(time, 2.));
float isOdd = step(mod(st.y * TILE_NUM * (1. - mode) + st.x * TILE_NUM * mode, 2.0), 1.);
st = translate(vec2(((isOdd * 2.) - 1.) * time) * vec2(1. - mode, mode) / TILE_NUM, st);
st = tile(TILE_NUM, st);
st = translate(vec2(.5), st);
st = scale(vec2(.5), st);
glFragColor = vec4(vec3(box(st)), 1.);
}
void example4(out vec4 glFragColor, float time, vec2 st) {
float TILE_NUM = 23.;
st = translate(vec2(0.5), st);
st = rotate(time, st);
st = translate(vec2(- 1. / TILE_NUM / 2.), st);
float tileDistance = length(floor(st * TILE_NUM))/ TILE_NUM;
st = tile(TILE_NUM, st);
st = translate(vec2(.5), st);
st = scale(vec2(clamp(0., 1.,1. - tileDistance * 2.)), st);
glFragColor = vec4(vec3(1. - box(st)), 1.);
}
void main() {
vec2 st = gl_FragCoord.xy/u_resolution;
example0(gl_FragColor, st);
example1(gl_FragColor, u_time, st);
example2(gl_FragColor, u_time, st);
example3(gl_FragColor, u_time, st);
example4(gl_FragColor, u_time, st);
}
|
下图为例子3和例子4。


圆形渐变半调子
“临摹”上面的第一张 SeExpr 作为结束。首先需要研究它们的效果。
第一张是圆形组成的半调子,能发现,每个圆形没有灰度变化,纯粹是根据每个小块黑白的比例来表示亮度的。
假设亮度从白到黑,圆形的大小从小到大的方向是 x 轴,垂直于此的方向为 y 轴,能发现 y 轴方向每一个圆形的间距都是一样的,显然,这里使用了 pattern 和距离场,x 轴方向越大就越暗。
但也能注意到,同一行中,随着 x 轴坐标变大,亮度并非是单调递增的,有时候会开一下倒车,这证明其中有一些随机性,但总体还是递增的。显然,对每一列,需要一个不同的亮度函数——想象柯里化,我们对每一列都构造一个这样的亮度函数。
但先忘记随机性,只考虑单调递增的情况。绘制这样的“单位”渐变的方法如下:
|
float magic(float colNum, vec2 st) {
vec2 dist = floor(st * (colNum)) / colNum;
st = fract(st * colNum);
float r = lumaFn(dist) * sqrt(2.) / 2.;
return step(r, distance(st, vec2(0.5)));
}
|
示例如下,有点丑,或许得调整这个亮度函数,但就这样了:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
| #ifdef GL_ES
precision mediump float;
#endif
uniform vec2 u_resolution;
#define PI 3.14159265359
vec2 translate(vec2 dir, vec2 st) {
return st - dir;
}
vec2 scale(vec2 ratio, vec2 st) {
return st / ratio;
}
vec2 rotate(float angle, vec2 st) {
return mat2(cos(angle),-sin(angle),
sin(angle),cos(angle)) * st;
}
float random (in vec2 st) {
return fract(sin(dot(st.xy,
vec2(12.9898,78.233)))
* 43758.5453123);
}
float noise (in vec2 st) {
vec2 i = floor(st);
vec2 f = fract(st);
float a = random(i);
float b = random(i + vec2(1.0, 0.0));
float c = random(i + vec2(0.0, 1.0));
float d = random(i + vec2(1.0, 1.0));
vec2 u = f*f*(3.0-2.0*f);
return mix(a, b, u.x) +
(c - a)* u.y * (1.0 - u.x) +
(d - b) * u.x * u.y;
}
float lumaFn(vec2 st) {
float noise = clamp(0., 1., noise(st * 2000.));
return clamp(0., 1., st.y + (noise - 0.4) * st.y);
}
float magic(float colNum, vec2 st) {
vec2 dist = floor(st * (colNum )) / colNum;
st = fract(st * colNum);
float r = lumaFn(dist) * sqrt(2.) / 2.;
return step(r, distance(st, vec2(0.5)));
}
void main() {
vec2 st = gl_FragCoord.xy/u_resolution.xy;
float COLNUM = 40.;
st = rotate(PI / 5., st);
st = translate(vec2(0., -.5), st);
float colX = floor(st.x * COLNUM) / COLNUM;
st = translate(vec2(0, colX / 5.), st);
st = st * 2.;
float n = magic(COLNUM, st);
gl_FragColor = vec4(vec3(n), 1.0);
}
|

当前学的东西其实非常有限,都是最基础的东西,但我意识到我不应该当前就去追求这种很“风格化”的东西,先把基础学好吧!之后或许会学一些 blender 和程序化建模来方便学习和实验,GLSL 和 SeExpr 就先这样了,已经收获足够多,必可活用于下一次。




















