import numpy as npimport pandas as pdimport timeimport seaborn as snsfrom typing import Callable , Tuple
神经元 神经元是神经网络中的基础单元,它包含输入,权重,偏置,输出,激活函数等概念;一个神经元有多个输入 ,每个输入端均有自己的权重 ,将神经元的每一个输入都和自己的权重相乘,将结果相加,最后再和偏置 相加,将结果传递给激活函数 ,得到的便是神经元的输出;神经元可以有多个输出,它们的值相同。使用代码表达的话,神经元的输出为:
def output (xs, ws, bs, activate_fn ):""" :param xs: 输入,为n维实数数组 :param ws: 权重,为n维实数数组 :param bs: 偏置,为实数 :param activate_fn: 激活函数 :return: 输出值 """ return activate_fn(xs.dot(ws) + bs)
在想象特定神经元的时候,应该想象神经元本身和它的输入,就像水母 。
激活函数 激活函数是接受实数返回实数的一元函数,激活函数不能是线性函数 (线性函数就是满足对任意a,b,有f(a + b) = f(a) + f(b)的函数,比如f(x)=2x),常用的激活函数有 sigmoid,ReLU等,它们的定义分别如下:
$$ sigmoid(x) = \frac{1}{1 + e^{-x}} $$
def sigmoid (x ):return 1 / (1 + np.exp(-x))def ReLU (x ):return np.max (0 , x)
神经网络 神经网络由多层神经元组成,一层神经元由多个神经元组成,第一层和最后一层称为输入层和输出层。神经网络的层数有多种计数方式,这里只计数拥有权重 的层。
假如上一层的输出为[x1, x2, x3],当前层有两个神经元,偏置和权重分别为w11, w12, w13, b1,w21, w22, w23, b2,则两个神经元的在执行激活函数前 的输出为:
a1 = x1 * w11 + x2 * w12 + x3 * w13 + b1a2 = x1 * w21 + x2 * w22 + x3 * w23 + b2
显然,这可以使用矩阵乘法和加法来描述:
[a1 , a2 ] = [x1 , x2 , x3 ] * [[w11 , w21 ], + [b1,w12 , w22 ], b2]w13 , w23 ]]
只需要将[a1, a2]中每一个元素执行一下激活函数即可得到该层的神经元的输出。这证明,除输入层以外,每一层神经元都可以用一个权重矩阵和一个偏置矩阵来表示。权重矩阵中,每个神经元的权重作为一列并横向拼接,偏置矩阵是一个每个神经元组成的行向量。输入和输出也是行向量 。输入层没有输入和偏置,它的输出由外界给定。
下面会将权重矩阵和偏置矩阵统称为权重矩阵。
输出层使用的激活函数可以与中间层不同,比如对分类问题,可以使用softmax函数,对回归问题,即根据已有的数据去预测 特定输入下的输出的问题,可以使用恒等函数。softmax的实现如下,它的性质是每个输出和该层其它神经元的输出相关联,所有神经元的输出总和为1,这让我们能够赋予每个神经元的输出以“概率”的语义。
$$ softmax(k) = \frac{e^{a_k}}{\sum_{i = 1}^{n} e^{a_i}} = \frac{Ce^{a_k}}{C\sum_{i = 1}^{n} e^{a_i}} = \frac{e^{a_k + \log_{}{C}}}{\sum_{i = 1}^{n} e^{a_i + \log_{}{C}}} = \frac{e^{a_k + C’}}{\sum_{i = 1}^{n} e^{a_i + C’}} $$
def softmax (x ):max (x)return exp_a / np.sum (exp_a)
前向传播 / 推理 把输入丢给神经网络,去获得它的输出,就是所谓的前向传播/推理,下面是一个三层神经网络(中间层第一、二层,输出层,这三层有权重)推理的函数:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 def predict (x, w1, b1, w2, b2, w3, b3, activate_fn, output_activate_fn = lambda x: x ):""" :param x: 输入 :param w1: 第一层的权重矩阵,列数为神经元的数量,行数为输入的数量 :param b1: 第一层的偏置行向量,大小为神经元数量 :param w2: 第二层的权重矩阵,列数为神经元的数量,行数为第一层的神经元的数量 :param b2: 第二层的偏置,大小为神经元数量 :param w3: 输出层的权重矩阵,列数为神经元的数量,行数为第二层的神经元的数量 :param b3: 输出层的偏置,大小为神经元数量 :param activate_fn: 中间层的激活函数 :param output_activate_fn: 输出层的激活函数,比如恒等函数 :return: 输出 """ return z3
梯度 导数,即函数在特定位置上的变化程度,根据数学公式去化简求导所求得的结果称为解析解,去近似地算出的结果称为数值解,数值解是很容易求的——给定尽量小的dx,求出(f(x + dx) - f(x)) / dx即可:
def numerical_diff (f, x, h=1e-4 ):""" 求函数f在位置x上的导数,该操作称为数值微分 numerical differentiation :param f: 一元函数 :param x: 函数入参 :param h: dx :return: 函数f在x处的导数 """ return (f(x + h) - f(x - h)) / (2 * h)lambda x: x ** 2 , 1 )
但光处理一元函数是不够的,我们需要处理多元函数的导数,即该函数对每一个参数的偏导数;求特定参数序列下任意一个参数的偏导数,就是固定其它参数,对该参数求导数,这个行为很像柯里化 。所有偏导数组成的序列称为梯度。
下面是求梯度的函数:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 def gradient (f, x, h=1e-4 ):""" :param f: 要求梯度的函数 :param x: 函数参数,以任意维数组的形式 :param h: dx :return: """ for i, _ in np.ndenumerate(x): 2 * h)return res
显然,该方法能够尽量减少对象拷贝,移动的损失,但它同时是线程不安全的,无法并发执行,将来必须改良。
梯度下降法 梯度表明了函数在当前“位置”上的运动的“趋势”,对每一个偏导数,当它大于0时,就意味着向该方向运动时,该方向的值会变大,小于0时,向该方向运动时,该方向的值会变小。这意味着,只要向梯度的符号相反的方向运动,值必定会减小,这意味着我们能够找到函数的(可能是局部也可能是全局的)最小值 (或者最大值,这无关紧要)。根据梯度找到函数的最小值的方法称为梯度下降法。
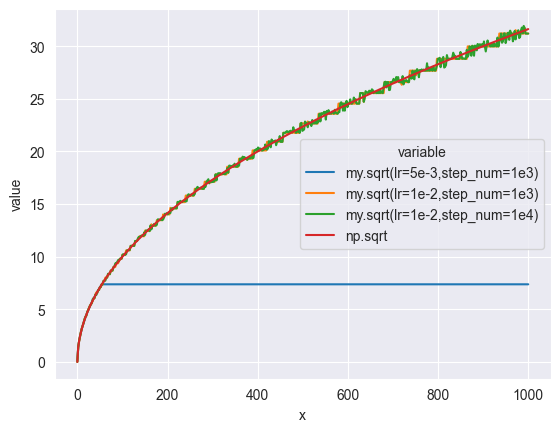
下面的函数使用梯度下降法实现了求解平方根,思路是构造这样一个函数,它的最小值即为所求的平方根,然后找到一个初始值,不断往梯度下降的方向去移动,最终会找到函数的局部或全局的最小值 :
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 def sqrt (x, lr=1e-3 , step_num=1000 ) -> float :""" 使用梯度法求平方根 :param x: 入参 :param lr: learn rate,学习率 :param step_num: 步数 :return: """ 1 ], dtype=np.float64)def h (_ ):return np.abs (x - d[0 ] * d[0 ])for _ in range (step_num):return d[0 ]def drawSqrt ():0 , 1000 , 500 )def sqrt (x,lr,step_num ):def h (d ):return np.abs (x - d * d)1 for _ in range (step_num):return d'x' : xs,'my.sqrt(lr=5e-3,step_num=1e3)' : sqrt(xs, lr=1e-3 , step_num=int (1e3 )),'my.sqrt(lr=1e-2,step_num=1e3)' : sqrt(xs, lr=1e-2 , step_num=int (1e3 )),'my.sqrt(lr=1e-2,step_num=1e4)' : sqrt(xs, lr=1e-2 , step_num=int (1e4 )),'np.sqrt' : np.sqrt(xs)'x' ), x='x' , y='value' , hue='variable' )
梯度下降法有两个超参数 (超参数即非神经网络通过训练得到,而是手动设定的参数):学习率和步数,学习率表示每次要向梯度下降的方向移动多大距离,步数表示移动的次数,学习率需要被合适地设定,过大和过小都会导致无法得到正确结果,比如上面的例子。
反向传播/神经网络的学习 正向传播就是把输入喂给神经网络,得到输出的过程,反向传播就是给定输入和期望的输出,根据期望的输出和实际的输出的关系去反向更新权重的过程 。神经网络中,可以使用梯度下降法进行反向传播。
首先需要定义我们需要应用梯度下降法的函数。该函数的参数为权重矩阵,返回值代表期望输出和实际输出的“距离” 。该函数称为损失函数 ,我们可以通过梯度下降法逐渐逼近损失函数的最小值,即让期望输出和实际输出最小的权重矩阵 ,一趟训练的一般过程如下,和sqrt的形式基本一致:
def train (W, x, t, lr, step_num ):def loss (W ):return distance(precict(x, W), t)for _ in range (step_num):return W
在实际操作中,我们不会对每一个训练数据都去进行梯度下降法,而是每次找到n个比如100个数据去做批处理,这既是去避免单个数据的特殊性,也能减少计算量。但同时也不会选择所有数据去进行学习,这又会增加计算量。每次随机选择特定数量的数据去训练的方法称为mini-batch,训练过程中使用梯度下降法进行反向传播,这整个称为随机梯度下降法SGD 。
损失函数 损失函数需要求得期望输出和实际输出的“距离”,在处理多个输出时,损失函数需要求得每一个输出的“平均损失”,这个除以N就行。
常用的损失函数包括均方误差,交叉熵误差,它们的定义如下:
$$ mean_squared_error(y, t) = \frac{1}{2}\sum(y_k - t_k)^2 $$
$$ cross_entropy_error(y, t) = -\sum_{k}^{} t_{k}\log_{}{y_{k} } $$
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 def mean_squared_error (y, t ):""" 均方误差,为“距离”的平方的一半 :param y: 实际输出 :param t: 期望输出 :return: """ return np.sum ((y - t) ** 2 ) / 2 def cross_entropy_error (y, t ):if y.ndim == 1 :1 , t.size)1 , y.size)0 ]return -np.sum (t * np.log(y + 1e-7 )) / batch_size
capstone 0: MNIST 识别手写数字 Hello, World! 这恐怕是最复杂的Hello World了。
MNIST数据集中的数据为28x28灰度像素表示的手写数字,其有60000条训练数据,10000条测试数据,每条数据包含该像素矩阵和对应数字值,下面拿它开刀,训练一个识别手写数字的神经网络。
数据文件从这里 下载,读取数据的代码拷贝自这里 。
首先设计神经网络的大小,这里设计一个两层神经网络(输入层,一个有权重的隐藏层,有权重的输出层),其中输入层的大小为28x28=784,即每个像素(这里丢掉长宽信息),第一个隐藏层为100个神经元,输出层为10个神经元,它们的输出分别表示数字为0-9的概率;隐藏层的激活函数使用sigmoid,输出层的激活函数使用softmax(这是个分类问题)。
在计算损失函数时,目标输出采用one-hot的形式,即只有一个元素为1的数组,如7会表示成[0, 0, 0, 0, 0, 0, 0, 1, 0, 0]。
一般流程如下:
设置超参数(批大小,训练次数,训练集大小,学习率) 随机抽取mini-batch 计算这批数据的损失函数的梯度 根据梯度和学习率更新参数 # 每一个mini-batch只移动一次梯度! 记录当前的损失函数的返回值供统计
整个代码实现如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 class TwoLayerNet :def __init__ (self, input_size: int , hidden_size: int , output_size: int , activation_function: Callable = sigmoid, loss_function: Callable = cross_entropy_error, output_activation_function: Callable = softmax ):def predict (self, x ):""" 正向传播 :param x: 入参数组,需为二维,每一行为一个输入 :return: """ return self.output_activation_function(t1 @ self.w2 + self.b2)def train (self, x, t, lr=0.1 ):""" 一次批训练,流程是根据输入,输出数据集去构造损失函数(它的参数是权重),然后求出此时的权重的梯度,将权重向梯度方向移动 需注意的是,这里对每一个mini-batch,只移动一次! :param x: 输入数据集 :param t: 期望输出数据集 :param lr: 学习率 :return: 当前的损失,以及梯度 """ def loss (_ ):""" 损失函数 :param _: 权重,这里通过闭包引入,在predict中被使用 :return: 当前权重下的损失 """ return self.loss_function(self.predict(x), t)return loss(0 ), (w1, b1, w2, b2)def accuracy (self, x, t ):""" 根据测试数据计算准确率 :param x: 测试数据输入 :param t: 测试数据期望输出 :return: """ 1 ) 1 )sum (y == t) / float (x.shape[0 ])return accuracy
下面加载数据集,让银河燃烧吧。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 import pickleimport osfrom mnist.MnistDataloader import MnistDataloaderdef readMnist () -> Tuple [np.ndarray, np.ndarray, np.ndarray, np.ndarray]:if os.path.exists('mnist/data.pickle' ):with open ('mnist/data.pickle' , 'rb' ) as f:return pickle.load(f)'mnist/train-images.idx3-ubyte' ,'mnist/train-labels.idx1-ubyte' ,'mnist/t10k-images.idx3-ubyte' ,'mnist/t10k-labels.idx1-ubyte' ).load_data()60000 , 784 )10000 , 784 )10 )[train_labels] 10 )[test_labels]with open ('mnist/data.pickle' , 'xb' ) as f:return res
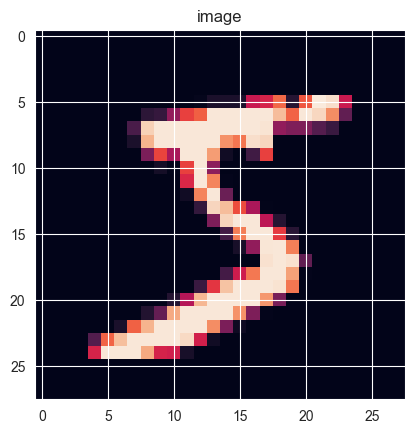
先检查一下是否正确读取了,读取一下第一张图片看看效果:
def img_show (img ):from PIL import Imageimport matplotlib.pyplot as plt'on' ) 'image' ) print (np.argmax(train_labels[0 ])) 0 ].reshape(28 , 28 ))
开干!下面的代码同样做了缓存,保证每次测试都能用上上一次的结果。
在执行该代码时,会发现其执行速率是极为缓慢的,瓶颈可能在计算梯度时,计算梯度的时候会对每一个参数进行两次前向传播,在这里每一次计算梯度需要进行 (w1.size + w2.size + b1.size + b2.size) * 2 = (784 * 100 + 100 * 10 + 100 + 10) * 2 = 159020次前向传播……这效率是令人崩溃的。因此这里修改了隐藏层神经元的数量到10,把计算量基本降低了一个数量级,但好像仍然跑的通??
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 0 ] 200 500 0.1 def doTraining ():def createNet ():if os.path.exists('mnist/net.pickle' ):with open ('mnist/net.pickle' , 'rb' ) as f:return pickle.load(f)784 , 10 , 10 )return netfor i in range (iter_num):print (f'{i + 1 } /{iter_num} : {end - start:.2 f} s, loss: {loss:.3 f} , acc: {net.accuracy(test_images, test_labels):.4 f} ' )with open ('mnist/net.pickle' , 'wb' ) as f:
这种全连接的,稀松平常的神经网络似乎称为MLP(多层感知机)。而这篇笔记或许就到这里了,因为下一章会对当前架构大改……看来这个是出不了成果了。但知识留着了。
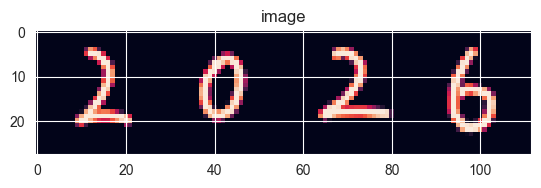
最后的最后,必须得拿真实的数据去实践一下,无论效果如何,下面是一张28x112的png文件,内容是手写的2026,看看我们的人工智障会输出什么东西。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 def split_image (image_path ):from PIL import Imageopen (image_path)for i in range (0 , height, 28 ):for j in range (0 , width, 28 ):28 , i+28 )for pixel in img.crop(box).getdata():round (0.299 * pixel[0 ] + 0.587 * pixel[1 ] + 0.114 * pixel[2 ])255 - np.array(gray_pixels))return np.array(result)'mnist/2026.png' )4 , 28 , 28 ), axis=1 ))with open ('mnist/net.pickle' , 'rb' ) as f:print (np.argmax(net.predict(images), axis=1 ))
哈哈哈哈哈哈哈哈哈哈哈哈哈