关于透视

该笔记记录了关于透视的心智模型，一些绘制透视图的准则，并简述了倍增线条、二等分、四等分、任意等分和透视中画圆的方法。

关于透视的心智模型

没看过多少材料，也不懂数学，这一节全程胡诌，注意甄别！例子均使用 blender 绘制。

透视是在二维的画布上展示三维物体的技术，可以通过计算机图形学（以及摄影？不知道呢）中的抽象来理解透视，并建立对透视的心智模型。

这里有三个概念：相机（camera），视口（viewport），对象（object）；相机不用解释，视口可以认为是相机的可视范围，也是我们的画面本身，它在这里是一个和相机有一定距离的矩形，其中相机在视口的投影为视口的中心。视口可以不是平面，通过改变平面的形状，我们可以得到其它类型的透视比如鱼眼透视，人眼是鱼眼透视。改变视口和相机的距离和视口的宽高比，我们就能得到不同的焦距；对象即为我们想绘制的对象，如立方体，球，少女等。

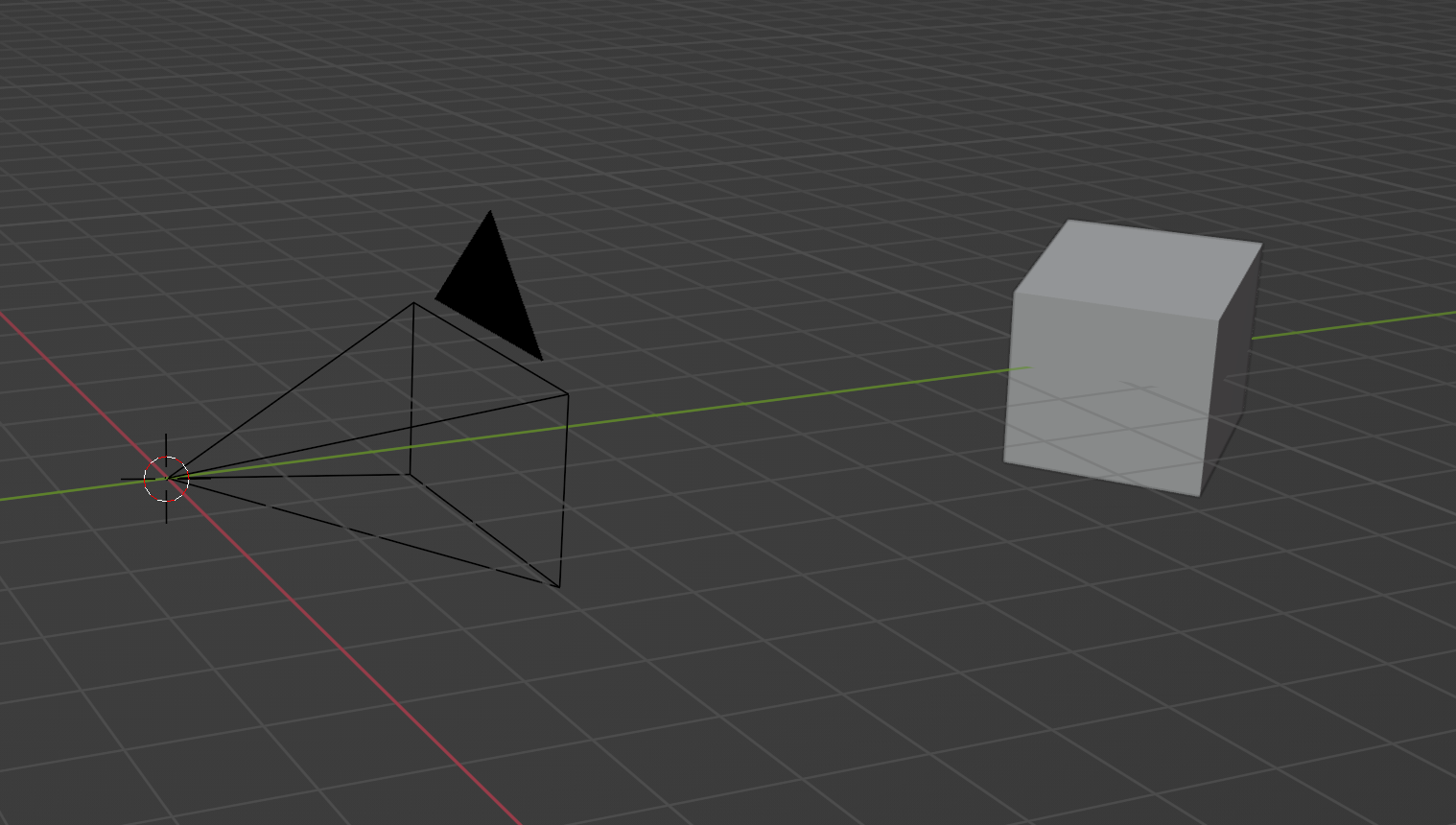
我们要绘制特定对象，就是做对象到相机在视口上的投影，具体来说，就是对对象的每个部分，做它和相机的连线，找到连线在视口上的交点。方法类似于下图（中心），但是投影面 P 在点和对象之间。

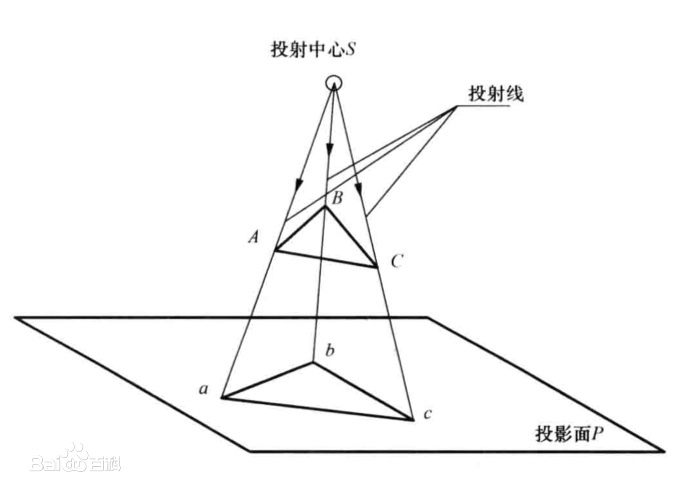
就是这么简单，只需要投影这一道工序，近大远小，消失点，一二三点透视，一切透视图的性质都自动地得到了。

近大远小

同一个对象，如果它正好在视口上，则它的投影大小（绘制的大小）和它本身一致；它离视口越远，它向相机在视口上的投影就会越小，这是符合直觉的。

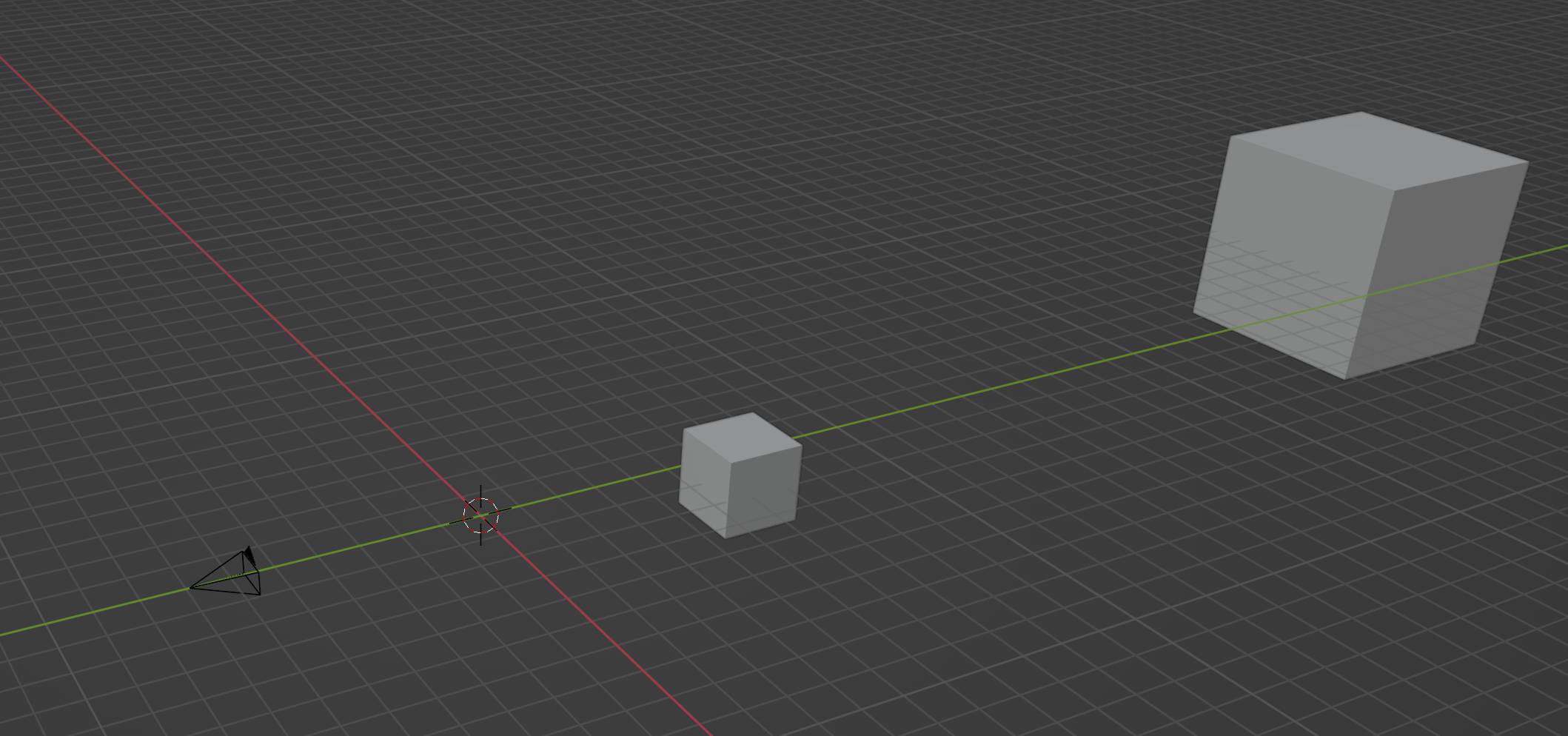
畸变

但一个很有趣的点是，如果这个物体始终在平行于视口的平面上运动，则（只要还在可视范围内，）它的投影大小是不会缩短的，甚至有可能会变大！下图是一个很明显的例子，这些球体的球心均在同一个平面上且半径相同，但形状完全不同：

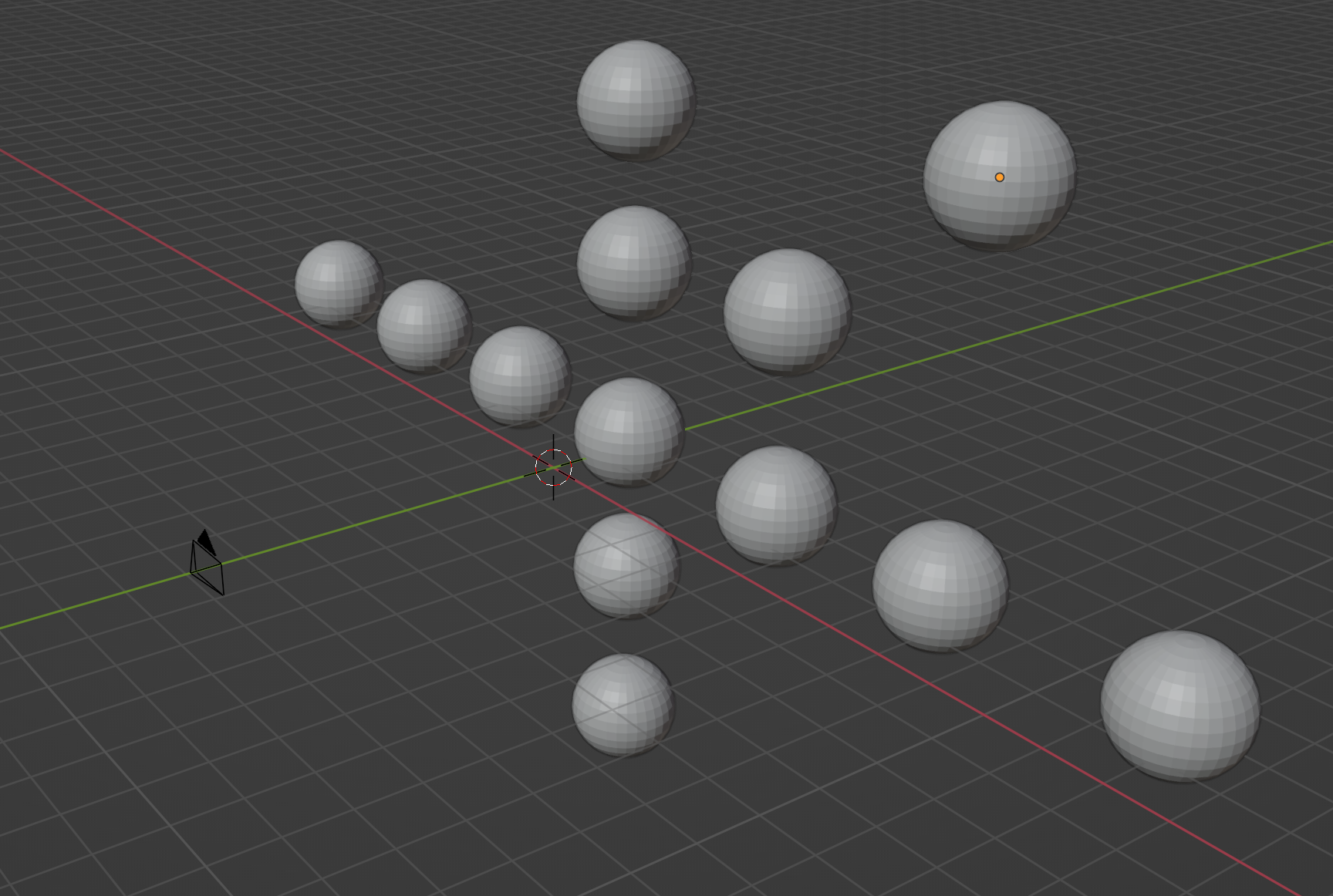
是谁说球在任何角度都是球的？

焦距：远处的变化小，近处的变化大

摄影中有所谓的长焦镜头，他们说，长焦镜头有“空间压缩”效果，变形幅度小，近大远小的感觉不明显。通过调整视口的大小，可以模拟长焦镜头的效果。

固定视口的宽高比和相机到视口的距离，则视场角（FOV，水平方向可视角度，常用在游戏里）和焦距成反比，下面展示了各视场角下同一个场景：

可以认为，不同视场角（焦距）下所看到的场景，就是去裁剪“原图”中间的部分并放大到原图的大小。

通过固定物体平行于视口方向的大小，并调整远离视口方向的大小，我们能够模拟不同焦距下的画面，这个可以应用在绘画中，它也证明，比较指向不同消失点的线段的长度是不可能的，因为它会随着焦距的大小而改变。

下面是不同焦距看同一张椅子：

也能认识到，当镜头距离物体非常远的时候，物体看起来就会像正视图一样了。

一点透视

当六面体的一个面平行于视口的时候，得到的就是一点透视，下面展示了低焦距和高焦距下的一些一点透视的正方体，其中高焦距将相机移远了。

平行于视口的线总是平行的

如果我们沿远离镜头的轴旋转一个六面体，则该六面体背后的面的边的方向如何确定？和面前的面的边平行。因为这两条边和视口平行且相互平行，因此投影到视口上仍旧是平行的。

二点透视

如果六面体只有一条边平行于视口，则我们得到二点透视。

下面的立方体均沿垂直方向旋转了 45 度：

三点透视

如果六面体没有任何面和边平行于视口，则得到三点透视。三点透视通常出现在非平视的情况，下面的图示在二点透视的基础上将相机的角度向下调整了 20 度，并向上移动了相机。

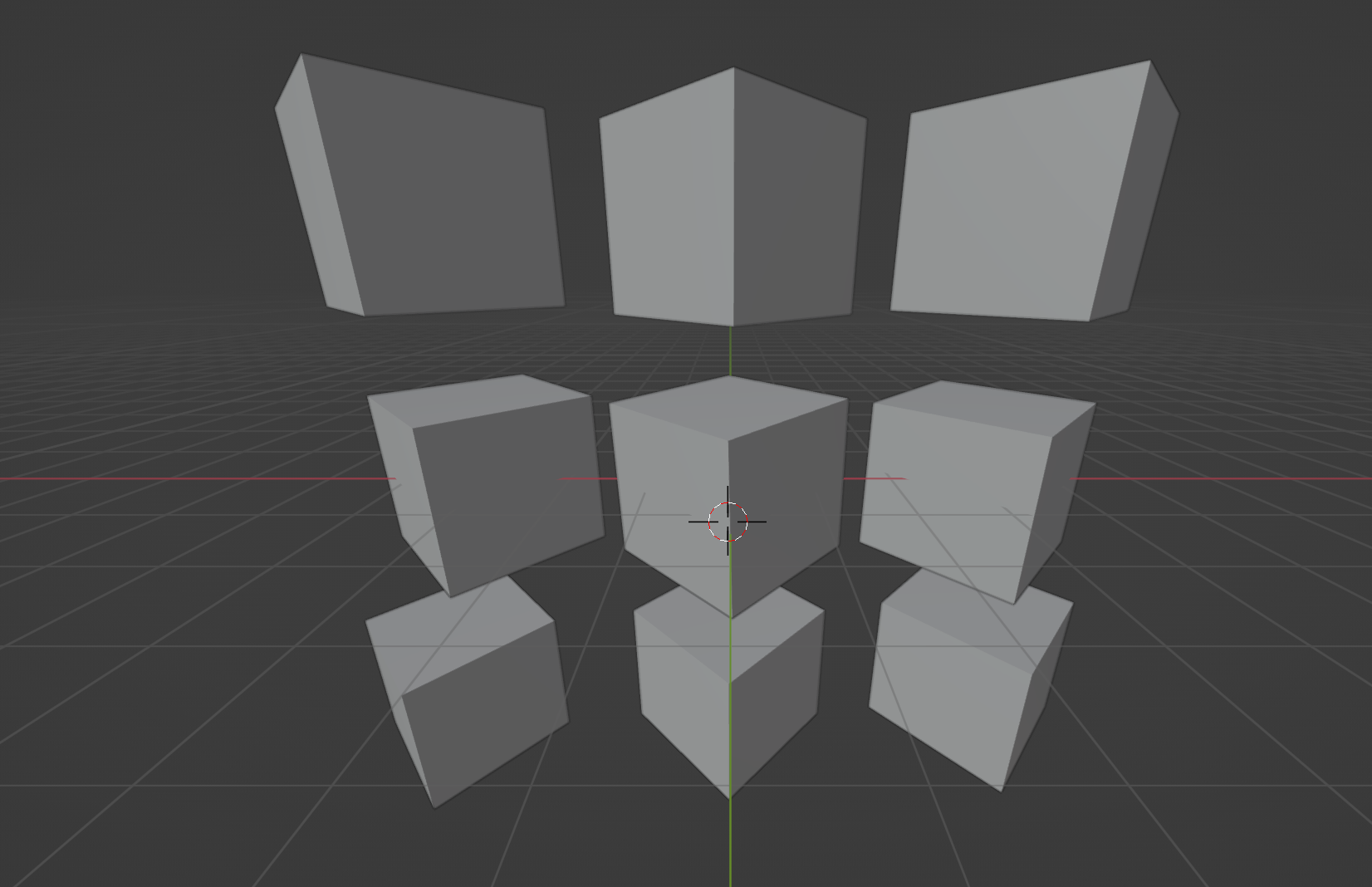
tips

1. 使用下面的画法的时候尽量减少测量次数以减少错误的累计，比如画等分时尽量把问题转化为画 2 的 n 次方等分
2. 始终关心视平线高度
3. 垂直消失点比水平消失点更重要（因为不同对象一般水平消失点不同，但垂直消失点相同）
4. 把要画的事物当成六面体（盒子）去看待
5. 始终使用近大远小的常识去检查画面是否正确，比如二分事物时，靠近镜头的部分会比远离对象的部分更大，猜测等分线的位置时也可以使用此种手段
6. 指向不同消失点的线段的长度是无法比较的，会随着相机的距离和 FOV（焦距）发生改变，因此选一个合适的比例并假定它们等长即可
7. 不要追求完全徒手绘画，该依赖工具就依赖工具，无论是透视尺还是 3d 辅助绘画，内容和效率最重要
8. 不要追求完全正确的透视，要为内容服务，如果画面需要夸张和扭曲，那就夸张和扭曲

一些透视画法

下面的透视画法中均依赖这样的假设：在平面作图中仅使用连线来进行的作图方法，在透视图中仍然适用，无论一点，二点，还是三点透视。无论这个假设是否为真，至少下面的画法的效果都还蛮符合直觉。

下面的画法均使用一个二点透视图做例子（这些画法都是在面上操作的，一个面显然最多是二点透视）。

要将这些画法应用到一点透视，把“做点到消失点的连线”修改为“过该点的边的平行线”即可。

二等分

因为倍增线段也需要用到二等分，这里先描述二等分画法。二等分就是将一个指向某消失点的线段分为等长的两段。

要进行二等分，只需对要操作的面的相对交点做连线，找两条连线的交点和消失线做直线，该直线即为等分线，其和面的边的交点即为等分点。

比如，要二等分 CD，则先连接 AC，BD，找到交点 E，直线 EY 即为二等分线，EY 和 AB，CD 的交点为二等分点；垂直方向的二等分点同理。

这个很容易证明，不表了。

倍增线段

倍增线段，该画法将一条指向消失点的线段长度增加一倍。它常用于“拷贝”等分点。

要做 DC 的倍增线段，需要找到 BC 的中点 E（在垂直方向上应用二等分），连接和延长 AE，AE 和 DC 的延长线交点为 F，则 DC = CF。

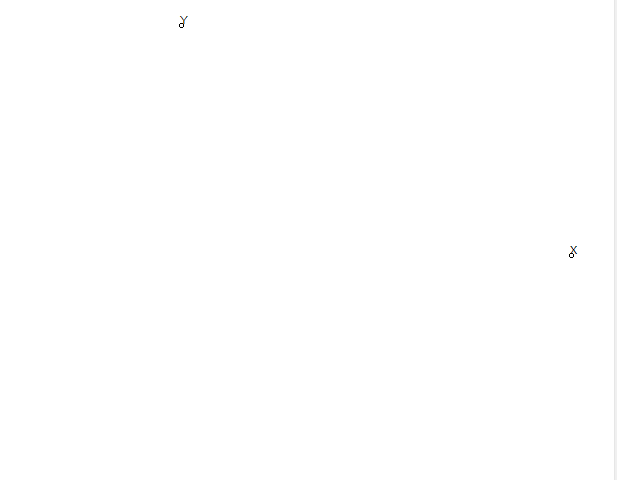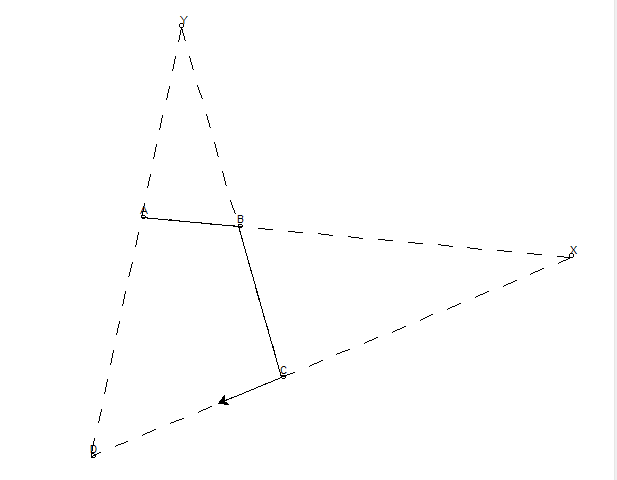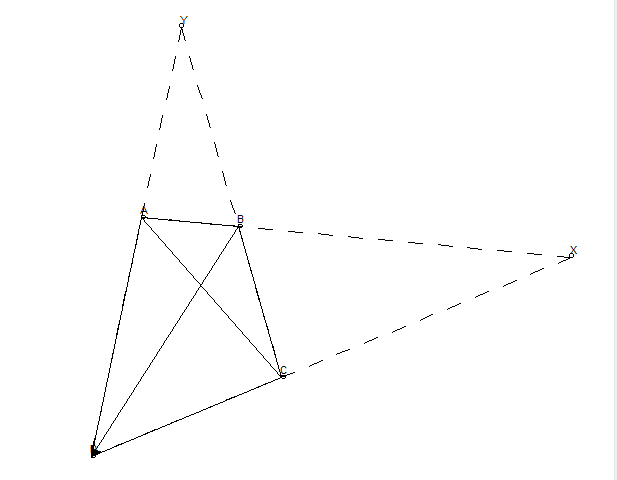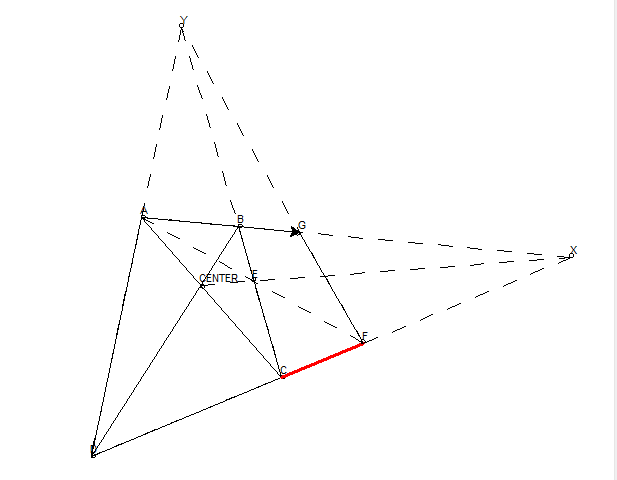
要证明 DC=CF，只需要证明三角形 BEA 和三角形 CEF 全等即可，这是容易证的。

四等分

四等分是容易的——做二等分后，前后再各做一次二等分即可。任意 2 的 n 次方等分均可如此。

任意等分

偶数等分在网络上都能查到很多资料，现在该来点魔法喽——精确地画出任意 n 等分，即使 n 是质数或任意奇数，这里直接给出规律——要找到 n 等分点，若 n 为偶数，则需要先找到 n/2 等分点（n 等分点可以在找到 n/2 等分点后再在前后进行一次二等分得到），若 n 为奇数，则需要先找到 n-1 等分点。这个方法是如此地机械化，以至于可以编程实现，下面是几种使用该方式的示例，分别使用 p5.js，geogebra，turtle 绘制。

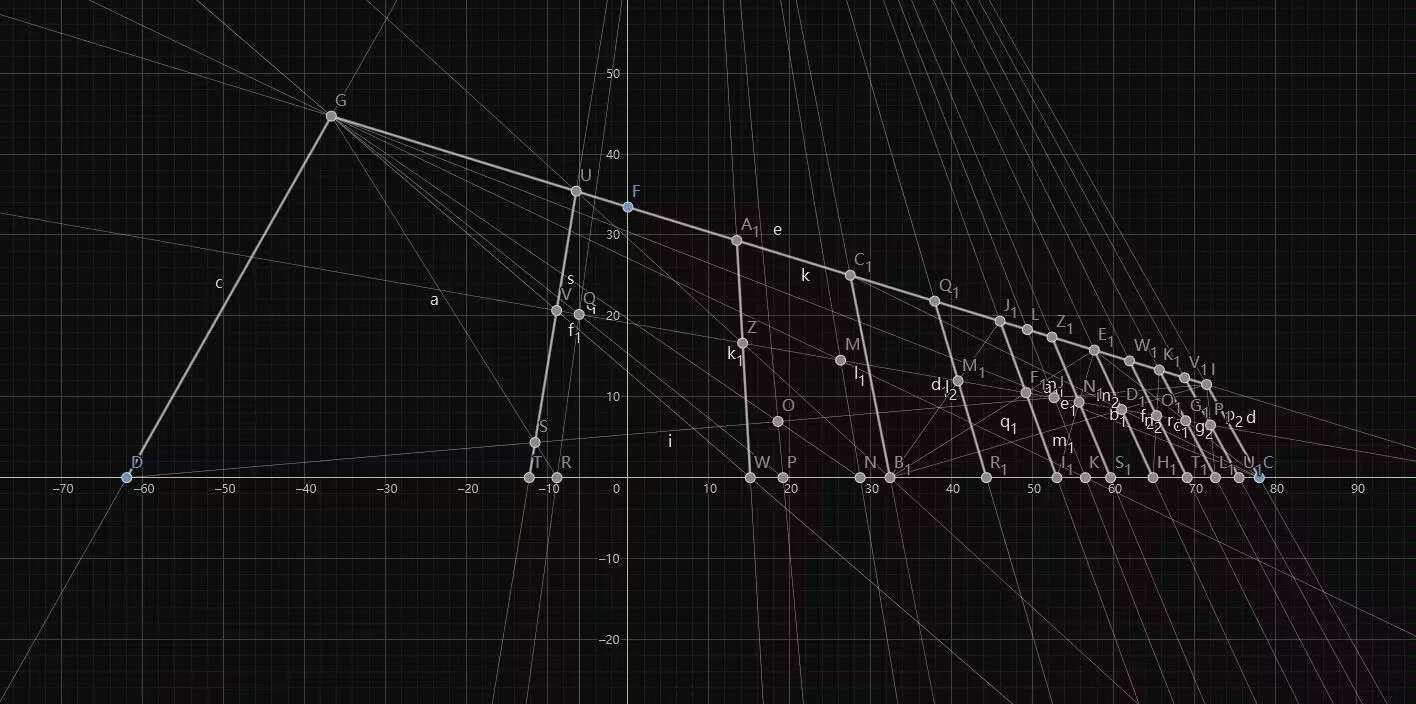
证明

现在试着证明，如果已经得到了 n 等分线，能仅通过连线（在平面情况下是做平行线，透视情况下是连接点和消失点）和找交点找到 n+1 等分线。

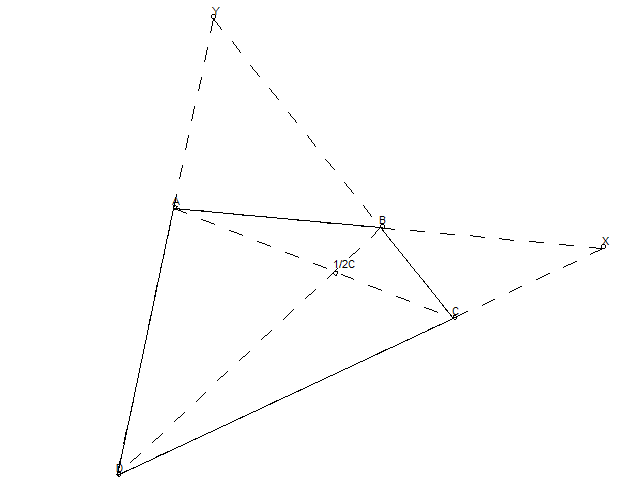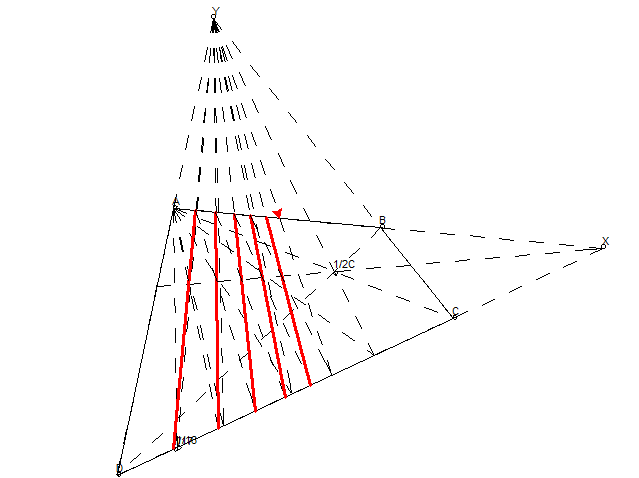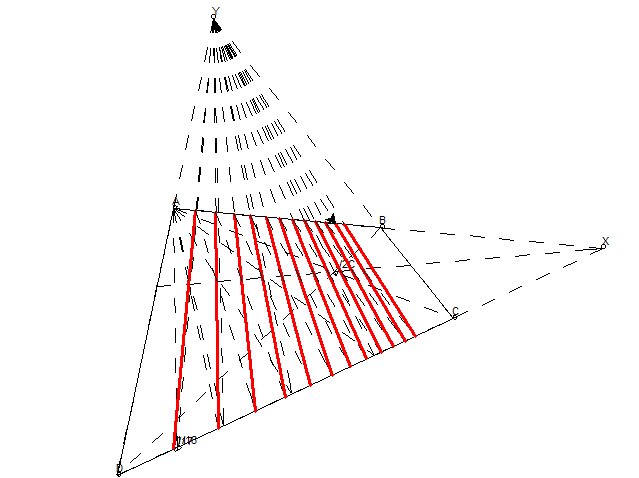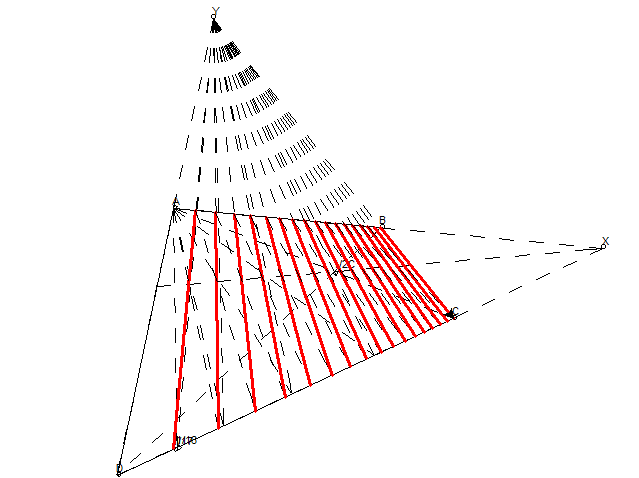
考虑下面的平面矩形，我们已经找到 n 等分线（EF），现在要找 n+1 等分点。连接 BD，AF，它们的交点在 n+1 等分线上，证明如下（不会 latex，手写了）：

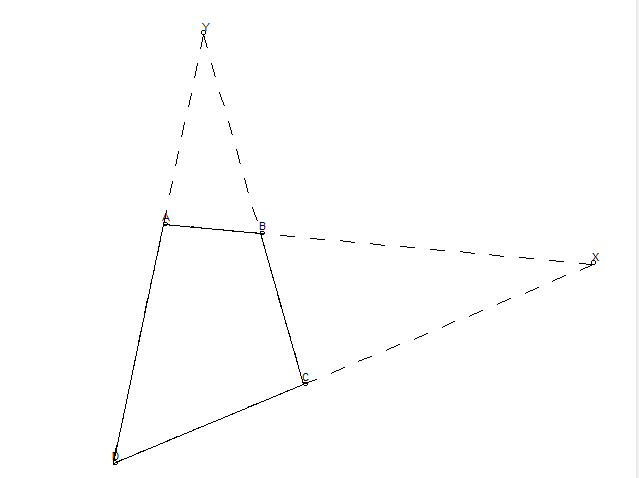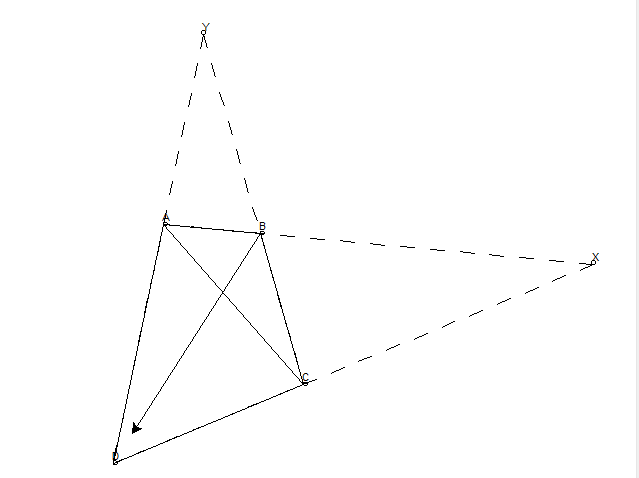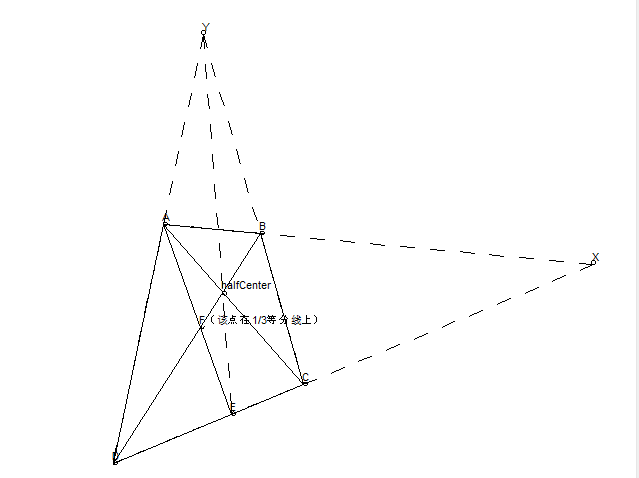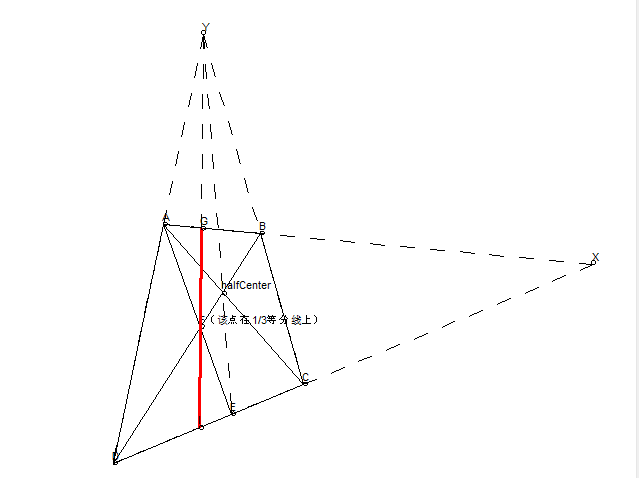
三等分

要找到三等分点，我们首先需要找到二等分线 EF，然后连接 AF，AF 和 BD 交点就在三等分线上。做完第一个三等分线后，可以使用倍增来找到第二个，或者对后三分之二这个矩形找二等分。

五等分

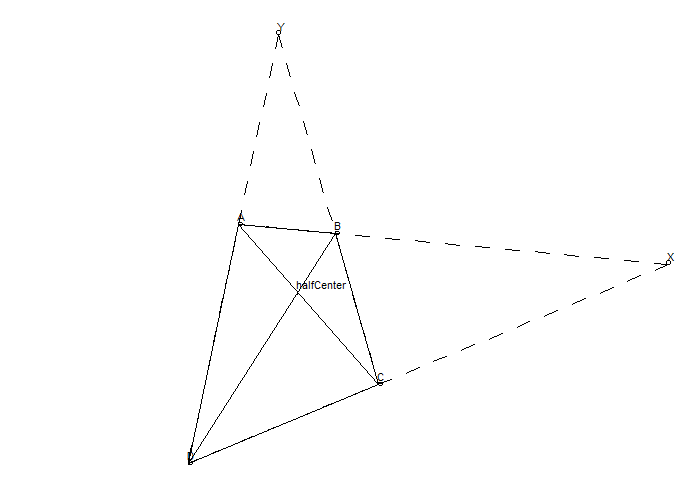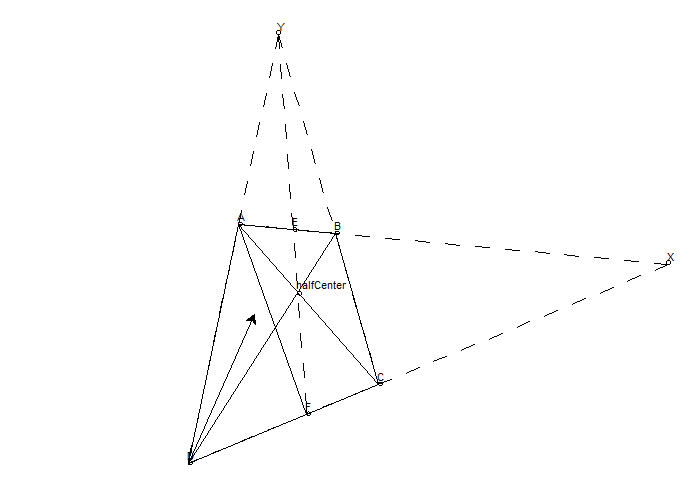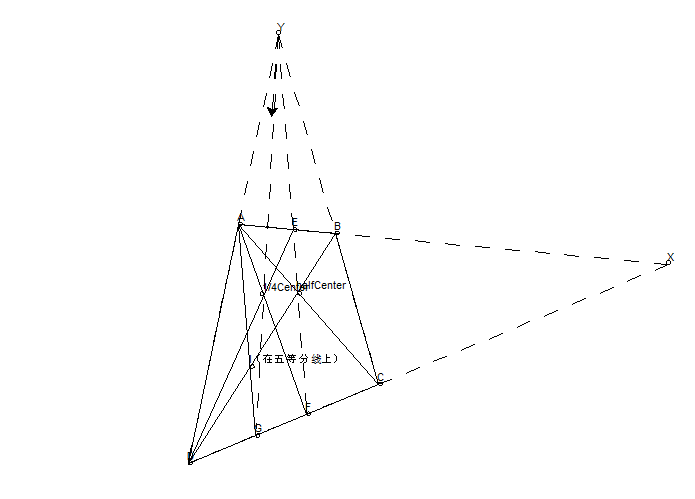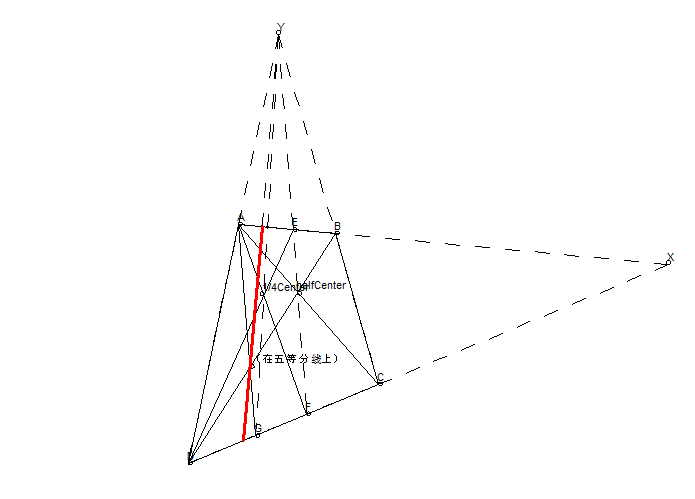
要找到五等分点，我们首先需要找到四等分线 EF（这是容易做的），然后连接 AF，AF 和 BD 交点就在五等分线上。做完第一个五等分线后，可以对后五分之四的矩形做四等分。

七等分

要找到七等分点，首先需要找到六等分线，要找到六等分线，首先要找到三等分线……以此类推。做完第一个七等分线后，对后七分之六点矩形做六等分即可，或者使用倍增法一步步推。

十一等分

剩余无论多少等分都是一样的操作，比如对十一等分，我们需要先找到十等分点，因此需要先找到五等分点，因此需要先找到四等分点……找到第一个十一等分线后，对后十一分之十的矩形做十等分即可。

透视圆的画法

不想写了，感觉这个没啥实践意义，留张图。

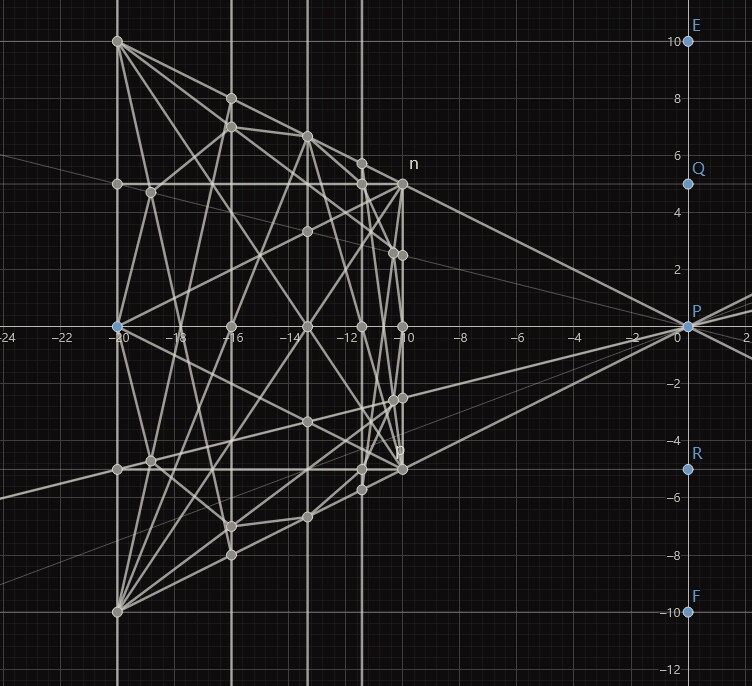
参考资料

• 《Computer Graphics from Scratch》
• https://coloso.global/en/products/illustrator_mogoon_us