lambda 实践

最近玩游戏 《Functional》，发现完全使用 lambda 做各种抽象还蛮有趣的，这里做一些关于实践 lambda 的笔记，顺路把 Y 组合子也给咔嚓掉——已经很长一段时间想要去学习它但搁置了。这里使用 js 去实现，它使用箭头函数时的语法已经足够简洁；所有 lambda 符号都写作λ，且所有字面量的 abstraction 都会给予括号。

回顾

这里先把 lambda 回顾一遍，在 lambda 中，存在着三种表达式——variable，abstraction，application。variable 的语法为任何小写字母，如 x，y，abstraction 的语法如λx.x，application 的语法如A B，其中 A，B 均为表达式。

下面都是合法的 lambda：

1
2
3
x
λx.xx
(λx.x) x

对 lambda，我们能做的唯一一件事其实就是化简，具体来说，是把 Application 化简；比如对(λx.x x) y，对其进行化简就是把 x 替换成 y，得到它的函数体，即y y。

最后是 abstraction 和 application 的结合性问题，abstraction 是右结合的，application 是左结合的，这就是说：

1
2
λx.λy.λz.xyz = λx.(λy.(λz.xyz))
x y z = (x y) z

从 js 的上下文来看，abstraction 就是函数定义，application 就是函数应用，下面均以此来称呼 abstraction 和 application。

哈吉马路哟！

Boolean

在一切开始之前，先预先定义一个 VOID 变量用于填充，它是一个 identity 函数：

1
VOID = λx.x
1
const VOID = x => x

布尔值是最简单的数据结构，它仅有两个值 True 和 False。

使用 Lambda 时，我们可以这样定义 Boolean：

1
2
TRUE = λa.λb.a  
FALSE = λa.λb.b

对应的 js 为：

1
2
const TRUE = a => b => a (VOID)
const FALSE = a => b => b (VOID)

这里其实我并不明确这里的 a 和 b 为何需要是函数，可能是为延迟求值，也可能是为统一“模式匹配”的形式（见下面的 部分总结），下面有些地方使用了这个形式，有些地方也没有。

它们的含义都很明确——TRUE 表示一个两参数的函数，返回第一个参数，FALSE 表示一个两参数的函数，返回第二个参数。可以认为，我们把 boolean 通过 lambda 去“编码”了。至于为何要这样编码，去问丘奇吧 hh。

这样抽象后，我们能够实现 if，if 是这样的结构——它接受三个参数，其中第一个参数是布尔值，若其为真，返回第二个参数，否则返回第三个参数，它的实现是显然的。

1
IF = λc.λa.λb. c a b
1
const IF = cond => a => b => cond(a)(b)

可以做一下演算，假设 1 和 2 是合法的 lambda 变量：

对其的使用类似这样：

1
2
3
console.log(
  IF (TRUE) (() => 1) (() => 2)
)

在这里，由于 javascript 的弱类型，可以注意到，IF 其实就是 identity 函数x => x——IF(TRUE)(1)(2) = TRUE(1)(2) = 1，IF(TRUE) = TRUE。

实现 AND 和 OR 也是简单的，它们的参数均为布尔值，返回值也为布尔值：

1
2
AND = λa.λb. IF a (IF b TRUE FALSE) FALSE
OR = λa.λb. IF a TRUE (IF b TRUE FALSE)
1
2
const AND = a => b => IF (a) (() => IF (b) (() => TRUE) (() => FALSE)) (() => FALSE)
const OR = a => b => IF (a) (() => TRUE) (() => IF (b) (() => TRUE) (() => FALSE))

Cons

Cons 的实现如下：

1
2
3
4
5
CONS = λa.λb.λn.λf.f a b
NIL = λn.λf.e
CAR = λp.p VOID (λa.λb.a)
CDR = λp.p VOID (λa.λb.b)
IS_NIL = λp.p TRUE FALSE
1
2
3
4
const CONS = a => b => onNil => onCons => onCons (a) (b)
const NIL = onNil => onCons => onNil (VOID)
const CAR = cons => cons (VOID) (a => b => a)
const CDR = cons => cons (VOID) (a => b => b)
1
2
const pairInstance = CONS (1) (2)
const car = CAR (pairInstance) // 1

Cons 的这个定义a => b => onNil => onCons => onCons (a) (b)十分有趣，我们可以给它加点括号来更突出这有趣之处：

1
const CONS = a => b => (onNil => onCons => onCons (a) (b))

可以建立这样的心智模型，即 CONS 是这样一个函数，它接受两个参数，去返回一个数据结构，而我们通过去传递给它一个“Matcher”（模式匹配）去获取该数据结构中的值。同时也可以注意到，NIL 的结构和调用 CONS 返回的数据结构是一致的。

然后，显然需要实现一个检查 PAIR 是否是 NIL 的函数，这个函数的实现同样很 trick 但能找到模式：

1
IS_NIL = λp. p TRUE (λa.λb. FALSE)
1
const IS_NIL = p => p (() => TRUE) (a => b => FALSE)

为何这么实现？推导一下就行了：

1
2
3
4
5
6
IS_NIL NIL
=> IS_NIL NOTHING
=> IS_NIL (λe.λf.e)
=> (λe.λf.e) TRUE (λa.λb. FALSE)
=> (λf. TRUE) (λa.λb. FALSE)
=> TRUE
1
2
3
4
5
6
7
IS_NIL (1, 2)
=> IS_NIL (CONS 1 2)
=> IS_NIL (λe.λf. f 1 2)
=> (λe.λf. 1 2) TRUE (λa.λb. FALSE)
=> (λf.f 1 2) (λa.λb. FALSE)
=> (λa.λb. FALSE) 1 2
=> FALSE

这很像模式匹配——只不过我们必须通过函数参数的形式去绑定所有值就是了，比如这个 IS_NIL 函数可以看成这样（使用 Scala 的模式匹配语法）：

1
2
3
4
match cons {
  case NIL -> TRUE
  case CONS(a, b) -> FALSE
}

Maybe

照葫芦画瓢，我们可以尝试去抽象 Maybe：

1
2
-- haskell syntax
data Maybe a = Nothing | Just a
1
2
NOTHING = λe.λf. e
JUST = λa.λe.λf. f a
1
2
const NOTHING = onNothing => onJust => onNothing (VOID)
const JUST = a => onNothing => onJust => onJust (a)

map 的操作如 map，flatMap，orElse 也可以定义出来：

1
2
3
IS_NOTHING = λm. m TRUE (λa.FALSE)
FLATMAP = λf.λm. m m (λa. f a)
MAP = λf.λm. m m (λa. JUST (f a))
1
2
3
4
const IS_NOTHING = maybe => maybe (TRUE) (a => FALSE)
const FLATMAP = f => maybe => maybe (() => maybe) (a => f (a))
const MAP = f => maybe => maybe (() => maybe) (a => JUST (f (a)))
const OR_ELSE = maybe => defaultValue => maybe (defaultValue) (a => a)

使用类似这样：

1
2
3
4
5
6
const a = JUST (1)
const b = MAP (x => x + 1) (a)

console.log(
    OR_ELSE (b) (-1000)
)

部分总结

在 haskell 中，Bool，Cons，Maybe，Either，Tree（二叉树）的类型定义分别如下：

1
2
3
4
5
data Bool = True | False
data List a = Cons a (List a) | Nil
data Maybe a = Just a | Nothing
data Either a b = Left a | Right b
data Tree a = Empty | Node a (Tree a) (Tree a)

使用 lambda 对其的抽象如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
TRUE  = λa.λb. a
FALSE = λa.λb. b

CONS = λa.λb.λn.λf. f a b
NIL  =       λn.λf. n

JUST    = λa.λn.λf. f a
NOTHING =    λn.λf. n

LEFT  = λa.λl.λr. l a
RIGHT = λb.λl.λr. r b

NODE  = λa.λb.λc.λe.λn. n a b c
EMPTY =          λe.λn.e

可以发现，对任何 ADT，它似乎都能通过 lambda 去抽象，其中，每一个值构造器对应一个函数，其接受值构造器的参数，去构造相应数据结构；然后，我们传递给这个数据结构一个 Matcher，对其进行“模式匹配”并获得值。

丘奇数

通过上面的观念，我们尝试操作一下自然数，皮亚诺自然数的 Haskell 定义是这样的：

1
data Nat = Zero | Succ Nat

定义相应 lambda，并去推演 ONE，TWO，THREE……

1
2
3
4
5
6
7
8
9
10
11
12
ZERO =    λx.λf. x
SUCC = λa.λx.λf. f a

ONE 
= SUCC ZERO
= (λa.λx.λf. f a) (λx.λf. x)
= (λx.λf. f (λx.λf. x))

TWO 
= SUCC ONE
= (λa.λx.λf. f a) (λx.λf. f (λx.λf. x))
= (λx.λf. f (λx.λf. f (λx.λf. x)))

但这样的自然数定义实在有点难以形容，这时候就来了丘奇数，它修改了 SUCC，把“Matcher”提前应用给了它的“值”：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
ZERO =    λx.λf. x
SUCC = λa.λx.λf. f (a x f)

ONE
= SUCC ZERO
= (λa.λx.λf. f (a x f)) (λx.λf. x)
= (λx.λf. f x)

TWO
= SUCC ONE
= (λa.λx.λf. f (a x f)) (λx.λf. f x)
= (λx.λf. f ((λx.λf. f x) x f)) 
= (λx.λf. f (f x))

THREE
= SUCC ONE
= (λa.λx.λf. f (a x f)) (λx.λf. f (f x))
= (λx.λf. f ((λx.λf. f (f x)) x f)) 
= (λx.λf. f (f (f x)))

可以发现，自然数的值就是 f 应用的次数，f 应用 n 次，则对应的自然数的值就是 n；其 js 表述如下：

1
2
const ZERO = x => f => x
const SUCC = a => x => f => f (a (x) (f))

根据丘奇数的形式，可以很容易地将丘奇数转换为 js 的数字：

1
2
3
function inc(n) {
  return n + 1
}
1
2
3
(λx.λf. f (f (f (f (x))))) 0 inc
= inc (inc (inc (inc (0))))
= 4

这种形式非常有趣，它像某种 reduce，其中 x 为初始值，f 为 step 函数，我们可以把 f 换成不同的函数（只要它的签名满足A => A），把 x 换成不同的值（即这里的类型A），比如我们可以去构造一个同这个自然数大小相同长度的列表：

1
2
3
function push0(x) {
  return [0, ...x]
}
1
2
3
(λx.λf. f (f (f (f (x))))) [] push0
= push0 (push0 (push0 (push0 ([]))))
= [0, 0, 0, 0]

这个性质对定义四则运算非常重要，比如考虑加法，对任意自然数 n，我们将其加 a，就是将其应用 a 次 SUCC，形式化地来说，就是：

1
PLUS n a = SUCC^a n

那么，如何在 n 上应用 a 次 SUCC 呢？答案很明白了：

1
PLUS = λn.λa. a n SUCC
1
const PLUS = n => a => a (n) (SUCC)

测试一下：

1
2
3
4
5
6
PLUS (SUCC (SUCC (SUCC ZERO))) (SUCC (SUCC ZERO))
= (λn.λa. a n SUCC) (SUCC (SUCC (SUCC ZERO))) (SUCC (SUCC ZERO))
= (SUCC (SUCC ZERO)) (SUCC (SUCC (SUCC ZERO))) SUCC
= (λx.λf.f (f x)) (SUCC (SUCC (SUCC ZERO))) SUCC
= SUCC (SUCC (SUCC (SUCC (SUCC ZERO))))
= 5

乘法也很简单——自然数 n 乘以自然数 a，就是0 + n + n + ... + n，其中 n 的个数为 a，我们只需要让 f 的值变为λx. PLUS x n即可，一个简单的闭包罢了：

1
MULTIPLY = λn.λa. a ZERO (λx. PLUS x n)
1
const MULTIPLY = n => a => a (ZERO) (x => PLUS (x) (n))

测试一下：

1
2
3
4
5
6
7
8
9
10
MULTIPLY (SUCC (SUCC ZERO)) (SUCC (SUCC (SUCC ZERO)))
= (λn.λa. a ZERO (λx. PLUS x n)) (SUCC (SUCC ZERO)) (SUCC (SUCC (SUCC ZERO)))
= (SUCC (SUCC (SUCC ZERO))) ZERO (λx. PLUS x (SUCC (SUCC ZERO)))
= (λx.λf.f (f (f x))) ZERO (λx. PLUS x (SUCC (SUCC ZERO)))
= (λx. PLUS x (SUCC (SUCC ZERO))) ((λx. PLUS x (SUCC (SUCC ZERO))) ((λx. PLUS x (SUCC (SUCC ZERO))) (ZERO)))
= (λx. PLUS x (SUCC (SUCC ZERO))) ((λx. PLUS x (SUCC (SUCC ZERO))) (PLUS ZERO (SUCC (SUCC ZERO))))
= (λx. PLUS x (SUCC (SUCC ZERO))) (PLUS (PLUS ZERO (SUCC (SUCC ZERO))) (SUCC (SUCC ZERO)))
= PLUS (PLUS (PLUS ZERO (SUCC (SUCC ZERO))) (SUCC (SUCC ZERO))) (SUCC (SUCC ZERO))
= + (+ (+ (0 2) 2) 2)
= 6

要定义减法，我们需要先定义 PRED 即前驱，减一操作，即从λx.λf. f (f x) 到λx.λf.f x。这个操作对皮亚诺自然数来说是非常容易的，但对丘奇数（，对我）来说完全不 trival，这里参考 如何理解丘奇计数的减法？ - Thomas Lin 的回答 - 知乎。

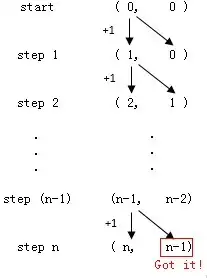
我们可以去尝试构造这样一个 PAIR 的序列，其中对每一个元素，它的第一个元素是第二个元素的后继，且对序列中后一个元素，它的第一个元素为前一个元素的第一个元素的后继，第二个元素为前一个元素的第二个元素；定义PRED ZERO = ZERO，依此定义这个序列的起始值为(ZERO, ZERO)；

根据示意图能发现，对任意自然数 n，只要找到这个序列中第 n 个值，它的第二个元素就是它的前驱。

因此，能够定义起始元素以及步进函数：

1
2
3
4
5
6
PAIR = λa.λb.λf.f a b
FST = λp. p (λa.λb.a)
SND = λp. p (λa.λb.b)

START = PAIR ZERO ZERO
STEP = λp. PAIR (SUCC (FST p)) (FST p)

根据上面的把自然数转换成 js 数字，列表的操作，我们同样可以把自然数直接转换成这个序列中的元素，只消 x，f 的值确定即可，其中 x 为 START（类型为(Nat, Nat)），f 为 STEP（类型为(Nat, Nat) => (Nat, Nat)），因此，要获取自然数的前驱，我们得到这样的代码：

1
PRED = λn. SND (n START STEP)

这里做一些测试：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
PRED ZERO
= SND (ZERO START STEP)
= SND ((λx.λf.x) START STEP)
= SND START
= SND (ZERO, ZERO)
= ZERO

PRED (SUCC ZERO)
= SND ((SUCC ZERO) START STEP)
= SND ((λx.λf.f x) START STEP)
= SND (STEP START)
= SND (STEP (ZERO, ZERO))
= SND (SUCC ZERO, ZERO)
= ZERO

PRED (SUCC (SUCC ZERO))
= SND ((SUCC (SUCC ZERO)) START STEP)
= SND ((λx.λf.f (f x)) START STEP)
= SND (STEP (STEP START))
= SND (STEP (SUCC ZERO, ZERO))
= SND (SUCC (SUCC ZERO), SUCC ZERO)
= SUCC ZERO

老实说，它的纯 lambda 形式我实在化简不下去了，这里直接开摆，把上面的 PRED 用 js 实现：

1
2
3
4
5
6
const PAIR = a => b => f => f (a) (b)
const FST = p => p (a => b => a)
const SND = p => p (a => b => b)
const START = PAIR (ZERO) (ZERO)
const STEP = p => PAIR (SUCC (FST (p))) (FST (p))
const PRED = n => SND (n (START) (STEP))

有了 PRED，我们能够定义减法了，自然数 n 减去自然数 a，就是 n 减去 a 次 1，即执行 n 次 PRED

1
MINUS = λn.λa. a n PRED
1
const MINUS = n => a => a (n) (PRED)

Y 组合子

这一节参考了https://stackoverflow.com/a/6713431和https://stackoverflow.com/a/6714066。

递归，也就是自己引用自己，比如下面的阶乘函数 fact，在其函数体中引用了自己：

1
2
3
function fact(n) {
  return n === 0 ? 1 : (n * fact (n - 1))
}

但在 lambda 演算中我们无法这样做，因为在 lambda 演算中不存在所谓的“名字”，因此无法直接去编写递归的函数；而通过 Y 组合子，我们便能在不引用自身的情况下编写递归函数，放到 js 的语境下，就是说我们能编写匿名的递归函数。

但在研究 Y 组合子之前，先来思考一下，怎样的情况下我们能让一个函数去不通过名字来引用自己？显然，这时候要拿到自己只可能通过两种方式——去捕获上层变量，或者去从函数参数中拿；其中后者的实现还是比较容易想到的——调用函数的时候，把自身传递过去就好了！比如这里编写一个 fib 函数：

1
2
3
4
5
const FIB = f => num => {
  if (num <= 1) return num
  return f(f)(num - 1) + f(f)(num - 2)
}
console.log(FIB(FIB)(10))

虽然乍一眼看起来有点作弊，但这是 lambda 可以实现出来的。我们考虑再来一个阶乘函数：

1
2
3
4
5
const FACT = f => num => {
  if (num === 0) return 1
  return f(f)(num - 1) * num
}
console.log(FACT(FACT)(10)) // 3628800

容易注意到，这玩意调用的时候是有特定的模式的——F(F)(...args)，我们将这个模式抽象一波：

1
2
3
4
5
6
const MAGIC = f => n => f(f(f))(n)
const FIB = MAGIC(f => num => {
  if (num <= 1) return num
  return f(f)(num - 1) + f(f)(num - 2)
})
console.log(FIB(10)) // 55

可以看到，这玩意已经部分能满足需求了，但蛋疼的一点是，在编写该递归函数的时候，每次调用自己都得写f(f)(...)，这比较麻烦，这种思考方式不可行。

现在回到递归函数，第一步，来写一个递归的 fact 函数：

1
2
3
function factorial(n) {
  return n === 0 ? 1 : factorial(n - 1) * n
}

第二步，我们可以把这个函数变成“Supplier”，这种形式和上面的显然是等价的，其中参数_显然被直接扔掉了：

1
2
3
4
5
function fact(_) {
  return n => n === 0 ? 1 : fact(_)(n - 1) * n
}

const factorial = fact(_) // _为任何值

第三步：直到上一步，事情还是 trival 的，函数仍旧引用了自己，为了解决这个问题，再抽象一层，我们可以把函数体里的fact(_)通过参数去传入，这要求_ = fact(_)，这里令_ = recur，得到recur = fact(recur)，将参数_替换为recur，将函数体中的fact(_)替换为fact(recur)，替换为recur，得到：

1
2
const fact = recur => 
  n => n === 0 ? 1 : recur(n - 1) * n

而 recur 的定义其实就是这个：recur = fact(recur)，这里引用了自己，所以必须要使用递归函数去定义；而且这不是 haskell，所以不能用 point-free 风格，这里必须要知道 recur 的类型，而这是容易看出来的：number => number，下面便是结果：

1
2
3
4
5
6
function recur(x) {
  return fact(recur)(x)
}

const factorial = fact(recur)
console.log(factorial(10))

好的，现在 fact 不是递归函数了，但我们又引入了一个新的递归函数 recur（欣慰的是，所有递归函数最后都能抽象成无显式递归的“body”和这样一个 recur 函数。

我们对 recur 采用和第一步到第二步同样的手段，即给它包一层 Supplier：

1
2
3
4
5
function recur(_) {
  return x => fact(recur(_))(x)
}
const factorial = fact(recur())
console.log(factorial(10))

然后，问题就在于如何处理_和recur(_)了，我实在弄不明白，把答案列出来：

1
2
const recur = f =>
  x => fact(f(f))(x)

虽然有点跳跃，但这里的 f，它就是 recur 本身：

1
2
const factorial = recur(recur)
console.log(factorial(10))

现在，所有的显式递归都已经移除，把最终的代码都列出来：

1
2
3
4
5
6
7
8
const fact = recur => 
  n => n === 0 ? 1 : recur(n - 1) * n

const recur = f =>
  x => fact(f(f))(x)
  
const factorial = recur(recur)
console.log(factorial(10))

容易发现，这里只有 fact 是“变”量，换成其它的递归函数，只有 fact 会改变，因此，我们将这个模式抽象出来，就得到了 Y 组合子：

1
const Y = fn => (f => x => fn(f(f))(x))(f => x => fn(f(f))(x))

它很容易使用 lambda 去表述：

1
Y = λfn. (λf.λx. fn (f f) x) (λf.λx. fn (f f) x)

这形式比想象中简单多了 hhh，可惜它的发明过程怕是值几篇博士论文吧？

Lazy List

有了 Y 组合子，现在可以自由地耍花活了，该操作操作列表了，但在此之前先和皮亚诺自然数过两招，不然列表存啥元素呢？这里首先给出皮亚诺自然数的定义，以及其到 javascript 数字类型的转换函数：

1
2
3
4
// Nat = Zero | Succ Nat
const ZERO = z => s => z
const SUCC = n => z => s => s(n)
const TO_NUMBER = Y(f => nat => nat(0)(pred => 1 + f(pred)))

皮亚诺自然数的加法也是简单的——对两个自然数a，b相加，检查a是否是ZERO，若是，则返回b，若不是，则令a为(SUCC c)，对c，(SUCC b)相加；乘法同样简单，对两个自然数a，b相乘，检查a是否是ZERO，若是，则返回ZERO，若不是，则令a为(SUCC c)，求c，b的乘积和b的和：

1
2
const PLUS = Y(plus => a => b => a(b)(c => plus(c)(SUCC(b))))
const MULTIPLY = Y(multiply => a => b => a(ZERO)(c => plus(b)(multiply(c)(b))))

这就足够了，下面实现列表相关操作，这里要求列表是惰性的，即 b 为返回 CDR 的函数，下面实现一下 map-filter-reduce，并实现 take 和 iterate，最终去实现一个自然数列表，取前 10 项奇数（本想取前 100 项，然而发现这爆栈了）的和；其中因为布尔值和自然数都未使用上面那种非严格求值的形式，这里定义了一个LAZY_IF来保证 if 为“短路”操作：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
const TRUE = a => b => a 
const FALSE = a => b => b 
const IF = cond => a => b => cond(a)(b)
const AND = a => b => IF(a)(IF(b)(TRUE)(FALSE))(FALSE)
const OR = a => b => IF(a)(TRUE)(IF(b)(TRUE)(FALSE))
const NOT = a => IF(a)(FALSE)(TRUE)

const Y = fn => (f => x => fn(f(f))(x))(f => x => fn(f(f))(x))

const ZERO =      z => s => z
const SUCC = n => z => s => s(n)
const PRED = nat => nat(ZERO)(pred => pred)

const IS_ZERO = nat => nat(TRUE)(() => FALSE)
const TO_NUMBER = Y(f => nat => nat(0)(pred => 1 + f(pred)))
const PLUS = Y(plus => a => b => a(b)(c => plus(c)(SUCC(b))))
const MULTIPLY = Y(multiply => a => b => a(ZERO)(c => PLUS(b)(multiply(c)(b))))

const EQUAL = Y(equal => a => b => 
  a(b(TRUE)(predB => FALSE))(predA => b(FALSE)(predB => equal(predA)(predB))))

const LAZY_IF = cond => a => b => cond(a)(b)()

const EQUAL1 = Y(equal => a => b => 
  IF (IS_ZERO(a)) 
    (IF (IS_ZERO(b)) (TRUE) (FALSE)) 
    (LAZY_IF (IS_ZERO(b)) (() => FALSE) (() => equal (PRED (a)) (PRED (b))))) 

const ONE = SUCC(ZERO)
const TWO = SUCC(ONE)
const THREE = SUCC(TWO)
const FOUR = SUCC(THREE)
const FIVE = SUCC(FOUR)

// 展示一波互调递归
const IS_EVEN_ = Y(isEven => isOdd => nat => LAZY_IF(IS_ZERO(nat))(() => TRUE)(() => isOdd(isEven)(PRED(nat))))
const IS_ODD_ = Y(isOdd => isEven => nat => LAZY_IF(IS_ZERO(nat))(() => FALSE)(() => isEven(isOdd)(PRED(nat))))

const IS_ODD = IS_ODD_(IS_EVEN_)
const IS_EVEN = IS_EVEN_(IS_ODD_)

// List a = Nil | Cons a (List a)
const NIL =            n => c => n
const CONS = a => b => n => c => c(a)(b)
const CAR = lst => lst()(a => b => a)
const CDR = lst => lst()(a => b => b())

// js 数组到 List
const TO_JS_ARRAY = Y(f => lst => lst([])(head => tail => [head, ...f(tail())]))

const MAP = Y(map => fn => lst => lst(NIL)(head => tail => CONS(fn(head))(() => map(fn)(tail()))))
const FILTER = Y(filter => fn => lst => lst(NIL)(head => tail => 
  LAZY_IF(fn(head))
    (() => CONS(head)(() => filter(fn)(tail())))
    (() => filter(fn)(tail()))))

const ITERATE = Y(iterate => seed => fn => CONS(seed)(() => iterate(fn(seed))(fn)))

const NAT_LIST = ITERATE(ZERO)(SUCC)

const ODD_LIST = FILTER(IS_ODD)(NAT_LIST)
const EVEN_LIST = FILTER(IS_EVEN)(NAT_LIST)

const FOLDL = Y(foldl => zero => fn => lst => lst(zero)(head => tail => foldl(fn(zero)(head))(fn)(tail())))
const SUM = FOLDL(ZERO)(PLUS)
const TAKE = nat => lst => LAZY_IF(IS_ZERO(nat))(() => NIL)(() => lst(NIL)(head => tail => CONS(head)(() => TAKE(PRED(nat))(tail()))))

const TEN = MULTIPLY(TWO)(FIVE)
const FIRST_TEN_ODD = TAKE(TEN)(ODD_LIST)

console.log(TO_JS_ARRAY(MAP(TO_NUMBER)(FIRST_TEN_ODD))) // [ 1, 3, 5, 7, 9, 11, 13, 15, 17, 19 ]
console.log(TO_NUMBER(SUM(FIRST_TEN_ODD))) // 100

就这样了，之后预备看《The Little Schemer》，多去了解一下递归，以及深入了解 Y 组合子。

参考资料

FP

本博客所有文章除特别声明外，均采用 CC BY-NC-SA 4.0 协议 ，转载请注明出处！