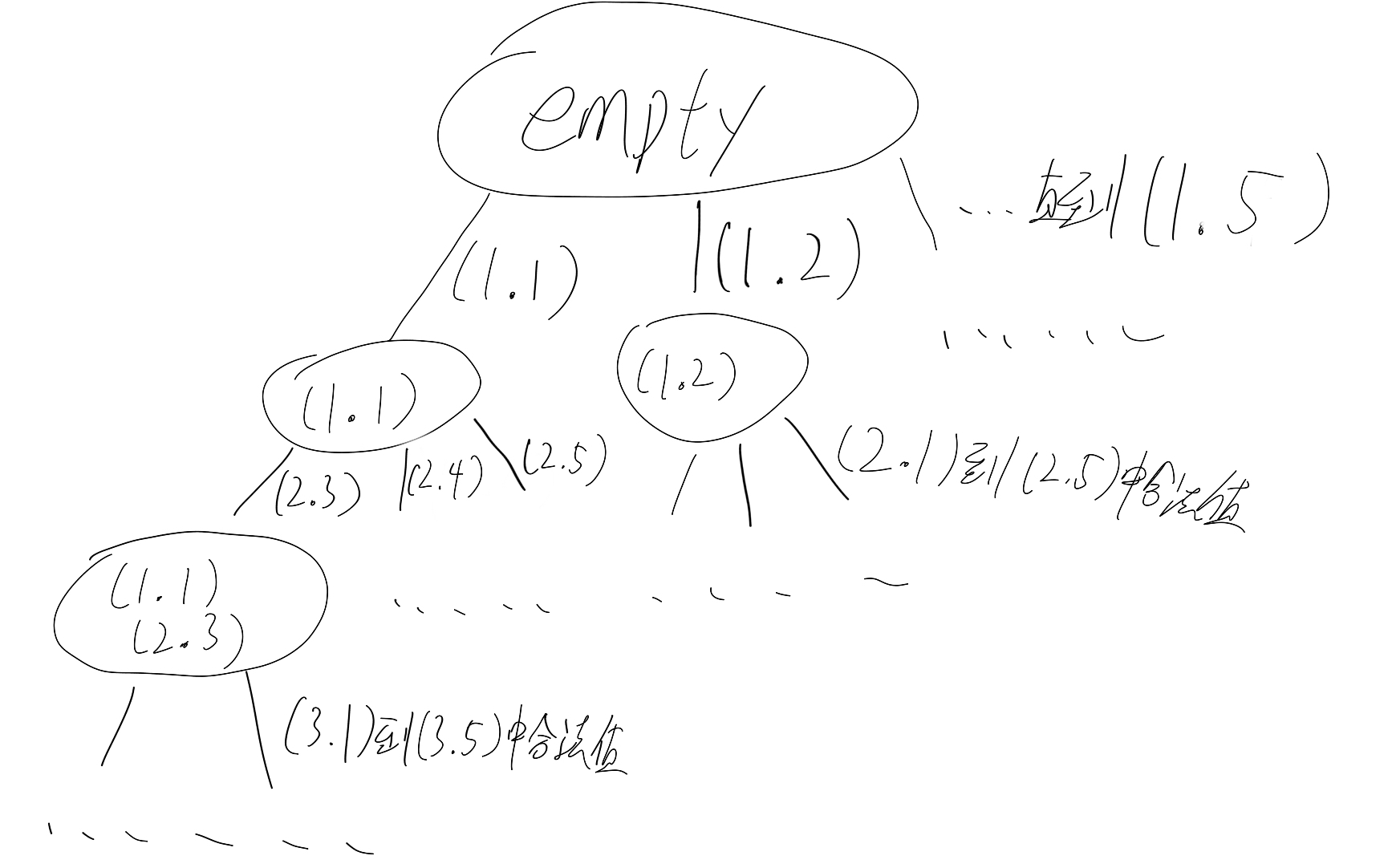2022 年 1 月 31 日更新，添加 Haskell 的解决方案，和 Racket 的实现一致（即“不断维护所有当前路径的列表”），但更容易看些。

permutationFrom1toN :: Int -> [[Int]]
permutationFrom1toN n | n <= 0 = error "!"
permutationFrom1toN n = helper (map pure [1 .. n]) 1
  where 
    helper :: [[Int]] -> Int -> [[Int]]
    helper lst step | step == n = lst
    helper lst step = lst >>= \ path -> 
      let validNextElem = filter (`notElem` path) [1 .. n] 
          nextPaths = map ((path ++ ). pure) validNextElem -- 不使用：是为了保证可读性
      in helper nextPaths $ step + 1

nQueens :: Int -> [[Int]]
nQueens n | n <= 0 = error "illegal argument"
nQueens n = helper (map pure [1 .. n]) 1
  where 
    helper :: [[Int]] -> Int -> [[Int]]
    helper pathList step | step == n = pathList
    helper pathList step = pathList >>= \ path ->
      let nextPaths = map ((path ++ ). pure) $ validNextPos path
      in helper nextPaths $ step + 1

    validNextPos :: [Int] -> [Int]
    validNextPos path = 
      filter (\currentX -> all (\(x, y) -> 
        currentX /= x && 
        abs (currentY - y) /= abs (currentX - x) 
      ) zippedWithY) [1 .. n]
      where zippedWithY = zip path $ iterate (+1) 1
            currentY = length path + 1

太久没有好好敲代码了……最近整一堆花里胡哨的，学 racket，haskell，scala（当然，日语也包含在内）之类的，但是一个都没深入。这里 racket 是我最感兴趣的，它的 LOP（面向语言编程）我非常想去了解和学习，scala 则是看重它运行在 JVM 上且有充足的函数式编程特性（函数式编程也是我想去了解的），在将来的项目中或许可以用到，haskell……新语法太多（但是它的函数的表现形式，对柯里化的支持等都是非常酷的…但是我苯，不想学：），还是纯函数式的，一时难以接受。

于是现在重拾算法，发现之前学的都不知道忘到哪里去了……是时候该进行一波复习了。首先拿 DFS 开刀，这算法是能归纳出一个“范式”的。

其实，无论 DFS 还是 BFS，其实都是以不同的方式遍历一棵树（也就是搜索的路径，其实也是在动态构造这棵树），那些没有叶子节点的节点即为搜索成功或再没有路径可选。区别在于，如果要留下搜索路径，BFS 需要保存所有的路径，而 DFS 则无此需要（可以说应该选择的路径被保存在函数调用栈中了）。从实例能看出这一点。

数的全排列

首先考虑数的全排列问题。这个问题要求给定一个数字 n，输出从 1 到 n 的全排列。

这里先按 BFS 来思考一下。假设 n 等于 3，能得到这样的一棵树——

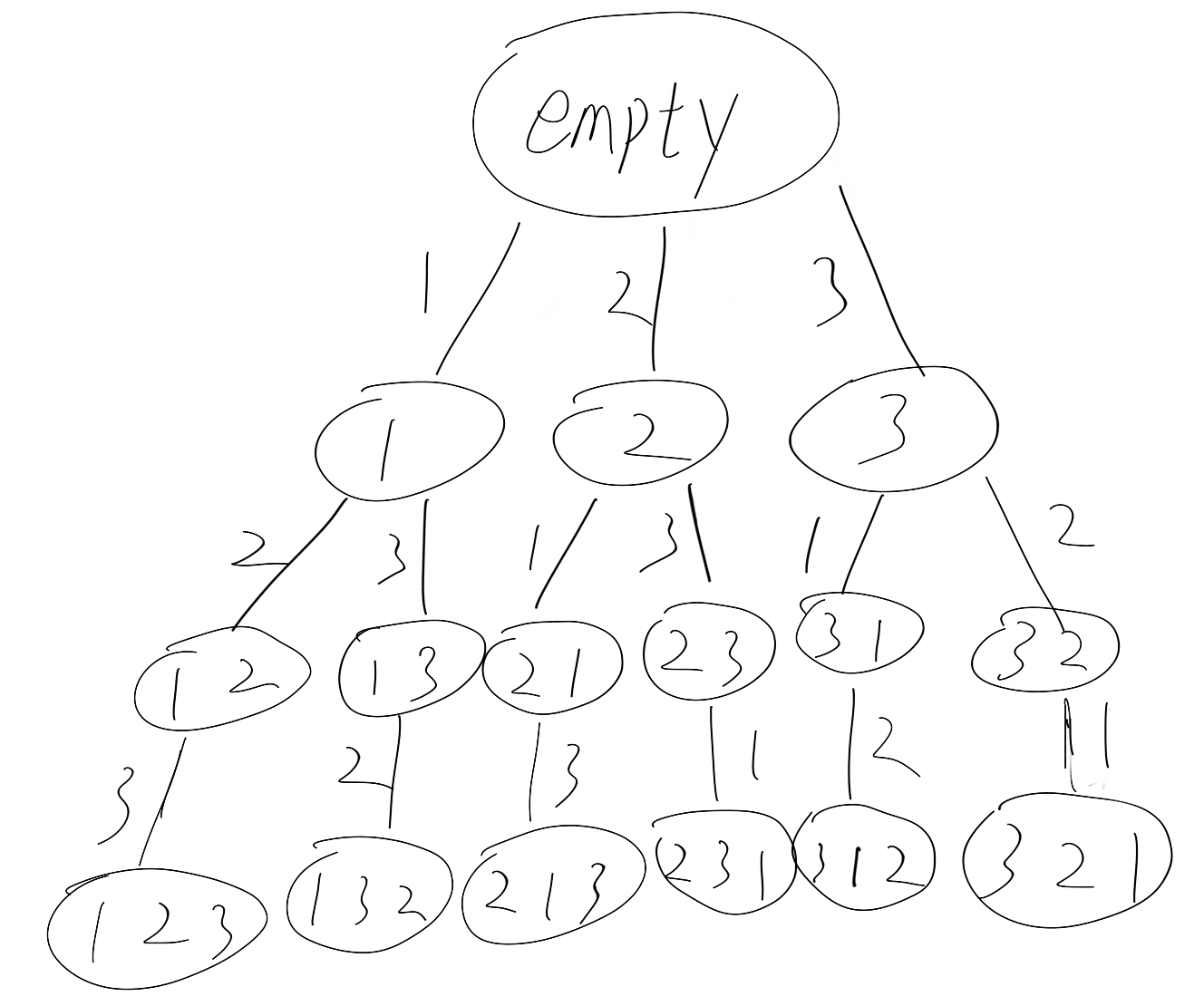
任何一个排列都是从根结点到子节点的一条路径。BFS 的方法就是不断维护所有路径，直到所有路径（或某个路径）成功（或失败）。

这个树叫解空间树，其实对树中每个节点（目前的路径），都需要遍历所有的可能（当然，也可以根据一定问题使用一定手段，以保证能在 O(n) 复杂度以下获取到有效可能），比如对路径 (1 2)，要遍历 1，2，3，然后发现 1 和 2 是不合法的，因此其子节点只有 (1 2 3) 了。

比如下面的 BFS 的 racket 实现就是不断维护所有当前路径的列表，假设 n 为 3，经历多次（n-1 次）迭代后，所有路径都到达终点，每次迭代的结果如下，其中 0 为初始值——

‘((1) (2) (3))
‘((1 2) (1 3) (2 1) (2 3) (3 1) (3 2))
‘((1 2 3) (1 3 2) (2 1 3) (2 3 1) (3 1 2) (3 2 1))

其实写完迭代的结果后我才突然意识到好像递归法满好写的…使用 map 和 flatten 就可以了，我用了非常丑陋的命令式的写法…

;; 写的累死人……我为啥不干脆用 Java 写？
;; BFS 的方法……由于我完全不熟悉 racket，所以写的及其丑陋（而且用了非常命令式的写法…由于 racket 并没有提供太多有副作用的函数，所以写的还是蛮痛苦的……这时候或许应该用 mutable list？）
;; 顺便，羡慕 haskell 的偏函数调用
(require control)
;; 以二维 list 的形式返回从 1 到 n 的全排列
(define (permutation-from-1-to-n n)
  ;; 从 (1) 到 (n) 的 list，它储存所有路径
  (define paths (build-list n (lambda (x) (list (add1 x)))))
  
  ;; 循环 n-1 次维护 paths，增长（和分支）其中每条 path 并将其“打散”到 paths 中
  (dotimes (__ (sub1 n))
    (set! paths (foldl append empty (map (generate-paths n) paths))))
  paths)

;; 一个柯里化函数，它维护和分支一条 path。比如对于 n=5，path=(1 3) 的情况，它返回 ((1 3 2) (1 3 4) (1 3 5))
(define generate-paths
  (lambda (n)
    (lambda (path)
      (for/list ([i (in-range 1 (add1 n))]
             #:when (not (member i path)))
    (append path (list i))))))

也可以使用队列来实现，其实质仍旧是不断维护所有当前路径，只不过将每次延伸队列头部的路径，并将其出队，将延伸后的路径加入到队列尾，容易知道当队列头部的路径长度为 n 时已获取到所有路径——

(require data/queue control)

;; 循环维护队列首，将其生成的路径入队，直到队首长度为 n，此时已生成所有全排列
(define (permutation-from-1-to-n n)
  (define res (make-queue))
  (for ([i (build-list n (lambda (x) (list (add1 x))))])
    (enqueue! res i))
  (while (not (= (length (queue-head res)) n))
    (for ([i ((generate-paths n) (dequeue! res))]) ; define 不能在循环体内使用
      (enqueue! res i)))
  (queue->list res))

;; racket 的 queue 居然没有提供直接获取队列头部的过程，设计者究竟是什么意思……
(define (queue-head queue)
  (let ([head (dequeue! queue)])
    (enqueue-front! queue head)
    head))

;; 同上面的定义
(define generate-paths
  (lambda (n)
    (lambda (path)
      (for/list ([i (in-range 1 (add1 n))]
             #:when (not (member i path)))
    (append path (list i))))))

DFS 相当与对每一条 path，对它的所有子节点进行“尝试”，DFS 解法的 racket 代码如下（这个比 Java 版好理解多了）——

(define (permutation-from-1-to-n n)
  (define (DFS path)
    (if (= (length path) n) ; 如果 path 长度已经为 n，说明必定已经完成一个排列。
        (println path) ; 基线条件，此时的 path 即为一条路经
        (for ([i (in-range 1 (add1 n))]) ; 从 1 到 n
          (unless (member i path)
            (DFS (append path (list i)))))))
  (DFS empty))

可以形象地将 DFS 解法的函数调用栈这样表示——

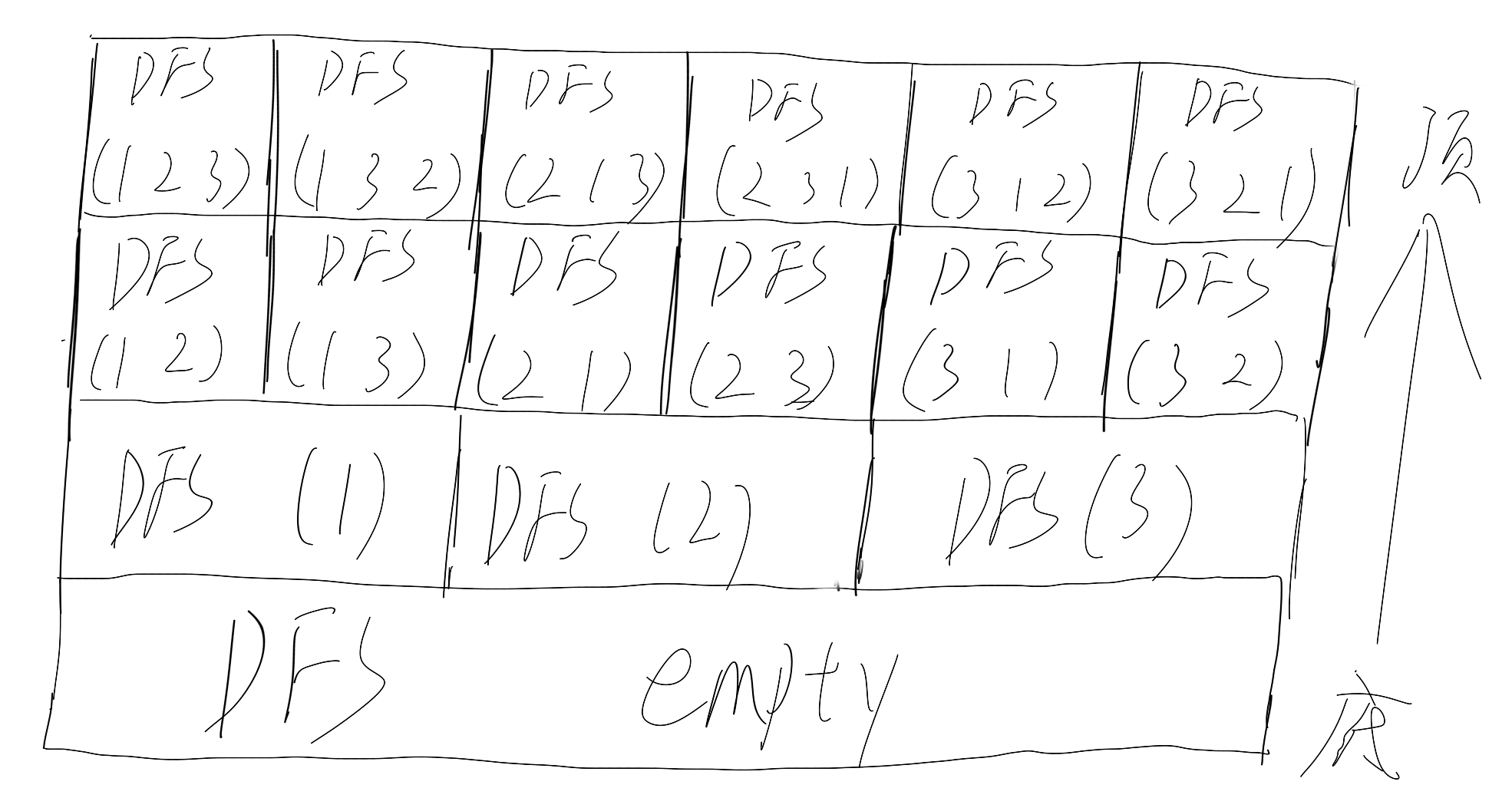
在每一次函数调用里，它都会对每一个可能进行递归，比如对路径’(1)，它会递归’(1 2)，’(1 3)……

Java 版的写法较此要麻烦一些（出于 Java 并不方便像 racket 这样的函数式语言一样使用不可变的数据结构），需要使用一个数组来维护当前路径，需要维护当前的“步长”。

public class Main {
    public static void permutationFrom1ToN(int n) {
        DFS(new int[n + 1], 1);
    }
    private static void DFS(int[] path, int step) {
        int N = path.length - 1;
        if (step == N + 1) { // 基线条件
            for (int i = 1; i <= N; i++)
                System.out.print(i + " ");
            System.out.println();
            return;
        }
        for (int i = 1; i <= N; i++) {
            // 传统手段是使用一个 bool 数组来维护元素是否已经保存在 path 中。如果使用那种方式，
            // 需要在将元素置入 path 前将该位置置为 true，在递归下一个位置后将该位置置为 false。
            // 这里直接通过一次遍历来检查元素是否存在于 path 中
            if (numInPath(path, step, i)) 
                continue;
            path[step] = i;
            DFS(path, step + 1);
        }
    }
    private static boolean numInPath(int[]path, int step, int num) {
        for (int i = 1; i < step; i++)
            if (path[i] == num) return true;
        return false;
    }
}

总之，DFS 可以归纳出一个“范式”——

def DFS(step):
    if （达到基线条件）:
        进行一些处理，比如打印，保存当前 path 等
        return

    for i in 所有元素 where i 未被取出且合法：# 遍历该 path 的下一步所有的可能
        books[i] = true # 取该元素
        path[step] = i
        DFS(step + 1) # 递归其子节点
        books[i] = false # 放回该元素

八皇后问题也是遵循这样的范式的。

八皇后问题

八皇后是这样一个问题——在一个 8X8 的棋盘上安排 8 个皇后，各个皇后两两之间要遵循这样的要求——每两个皇后不能在同一行，同一列，或相对棋盘边相互呈 45 度（即行距离和列距离相等）。

一个问题是，如何定义“步长”？这里考虑到各个皇后两两不能在同一行同一列，但每一行，每一列又必须存在一个皇后，所以可以以行数或列数作为步长。比如对一个 5X5 的棋盘，可以有这样的树，其中 (1 . 1) 这样的值代表在位置 (1, 1) 安放皇后——

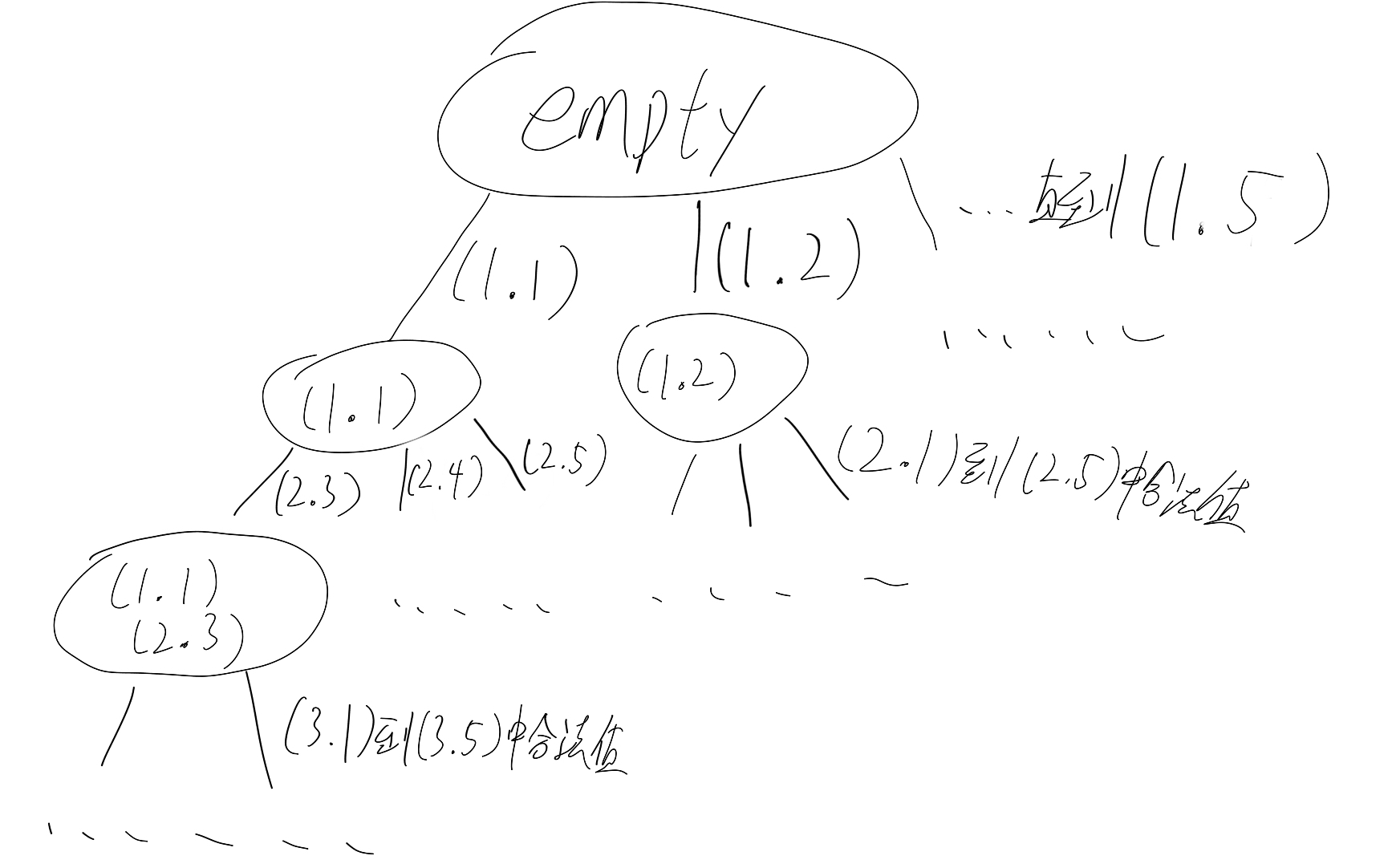
其实就根本上来说，步长是每一个皇后的安置，也就是说每一步都可以遍历整个棋盘，检查该位置是否可以安置皇后，但是这样是不划算的——已经安置过皇后的行或列是不必要再遍历的，并且会造成有重复的情况。比如对路径’((1 . 1) (2 . 3) …)，还可以有路径’((2 . 3) (1 . 1) …)……

因此，可以很容易得到 DFS 的代码，这里以行作为 step——

// 一年后再看这代码，只能说很面向过程😂
class Queen {
    public int step;
    public int y;

    Queen(int step, int y) {
        this.step = step;
        this.y = y;
    }
}

public class Main {
    private static int counter = 0;

    public static int n_queensCount(int n) {
        counter = 0;
        DFS(new Queen[n + 1], n, 1);
        return counter;
    }

    private static void DFS(Queen[] queens, int n, int step) {
        int N = queens.length - 1;
        if (step == N + 1) { // 基线条件
            counter++;
            return;
        }

        for (int i = 1; i <= n; i++) { // 从第一列到第 n 列，这里的行数是 step
            if (!canPlaceAt(step, i, queens)) // 遍历第 1 到第 step-1 个 queen，看这个 queen 能不能放在这里
                continue;
            queens[step] = new Queen(step, i);
            DFS(queens, n, step + 1);
        }
    }

    private static boolean canPlaceAt(int step, int y, Queen[] queens) {
        for (int i = 1; i <= step - 1; i++)
            // 如果在同一列或对角线
            if (y == queens[i].y || 
                Math.abs(step - queens[i].step) == Math.abs(y - queens[i].y))
                return false;
        return true;
    }
}

racket 代码如下（can-place? 过程给我写麻了…），仍旧以行作为 step——

(define-struct queen (step y) #:transparent)
; 判断 (step . y) 位置是否合法
(define (can-place? path step y) ; 只要既有的 path 中没有和要放置的 path 处于同一行，同一列或对角线，则合法
  (andmap 
    (λ (queen)
      (and (not (= (queen-y queen) y))
           (not (= (abs (- (queen-step queen) step))
                   (abs (- (queen-y queen) y))))))
    path))

(define (n-queens n)
  (let DFS ([path empty])
    (define step (add1 (length path)))
    (if (= (length path) n)
        (println path) ; base case
        (for ([y (in-range 1 (add1 n))]) ; 迭代从 1 到 n 列
          (when (can-place? path step y)
            (DFS (append path (list (make-queen step y)))))))))

哦瓦！

算法

本博客所有文章除特别声明外，均采用 CC BY-NC-SA 4.0 协议，转载请注明出处！

工厂方法模式和抽象工厂模式上一篇

面向对象七原则，单例模式，简单工厂模式下一篇

DFS 从入门到入坟——全排列和八皇后问题

数的全排列

八皇后问题